- 题目链接:上帝造题的七分钟2 / 花神游历各国
- 题目标签:线段树
- 题目大意:给定一个序列,有两种操作,一种是区间求和,另一种是区间修改(全部开平方)。
- 题目思路:肯定用线段树来修改数值,但如果按照常规修改肯定会TLE,那我们就应该进行优化。
- 我们来思考一下如何优化,假如我们现在有一个很大的数,经过多次开方,肯定会变为1或0。
- 看一下图
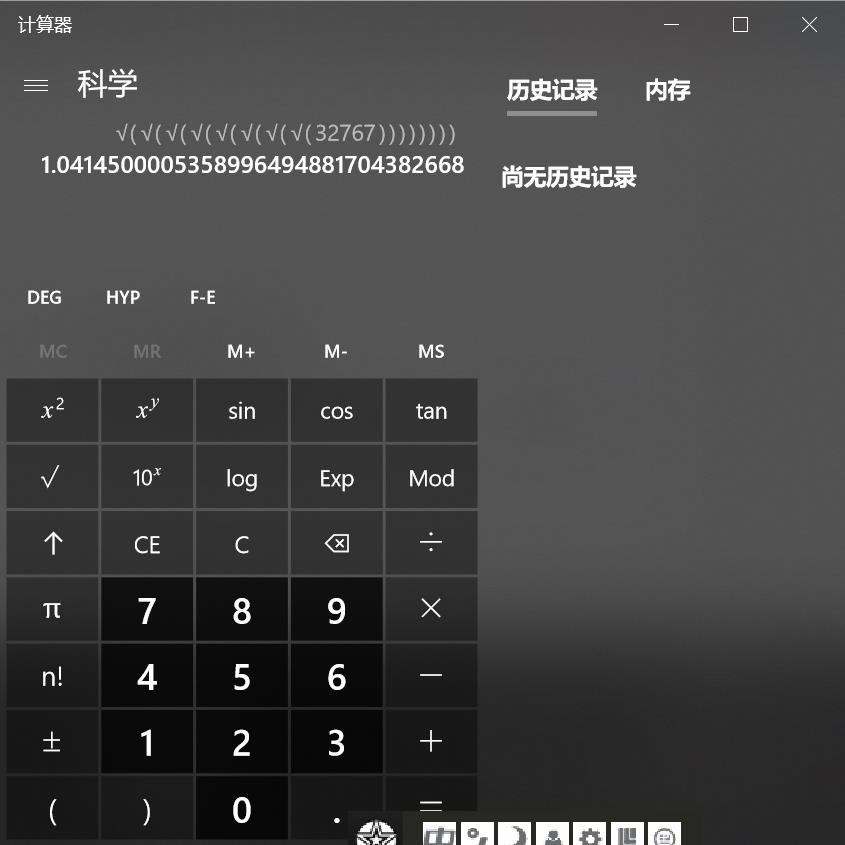
- 所以我们只需要设置一个bool数组来判断这个数值是否为1就可以完美解决修改超时的问题。
- 温馨提示:在区间求和时,给出的l和r可能会l>r,要进行判断。
代码就带不解释了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
using namespace std;
typedef long long ll;
ll sc() {
ll xx=0,ff=1; char cch;
while(cch<'0'|| cch>'9') {
if(cch=='-') ff=-ff; cch=gc;
}
while(cch>='0'&& cch<='9') {
xx=xx*10+(cch-48); cch=gc;
}
return xx*ff;
}
ll n,m;
ll a[Maxn],sum[Maxn*4];
bool vis[Maxn*4];
namespace DY {
void modify(ll k,ll l,ll r,ll x,ll y) {
if(vis[k]) return ;
if(l==r) {
sum[k]=sqrt(sum[k]);
if(sum[k]==0|| sum[k]==1) vis[k]=1;
return ;
}
ll mid=l+r>>1;
if(x<=mid) modify(k<<1, l, mid, x, y);
if(y>mid) modify(k<<1|1, mid+1, r, x, y);
sum[k]=sum[k<<1]+sum[k<<1|1];
vis[k]=vis[k<<1]&&vis[k<<1|1];
}
ll query(ll k,ll l,ll r,ll x,ll y) {
if(l>=x&& r<=y) return sum[k];
ll mid=l+r>>1,ans=0;
if(x<=mid) ans=query(k<<1, l, mid, x, y);
if(y>mid) ans+=query(k<<1|1, mid+1, r, x, y);
return ans;
}
void build(ll k,ll l,ll r) {
if(l==r) {
sum[k]=a[l];
if(sum[k]==0|| sum[k]==1) vis[k]=1;
return ;
}
ll mid=l+r>>1;
build(k<<1, l, mid);
build(k<<1|1, mid+1, r);
sum[k]=sum[k<<1]+sum[k<<1|1];
vis[k]=vis[k<<1]&&vis[k<<1|1];
}
void main() {
n=sc();
for(int i=1; i<=n; i++)
a[i]=sc();
build(1,1,n);
m=sc();
while(m--) {
ll flag=sc(),u=sc(),v=sc();
if(u>v) swap(u,v);
if(!flag) {
modify(1,1,n,u,v);
}
else {
printf("%lld\n",query(1,1,n,u,v));
}
}
}
};
int main() {
DY::main();
return 0;
}