- 题目链接:零点
- 如果没有权限看题,请看下图


- 题目思路:就是模拟了,根据题意模拟即可,具体解释见代码。
- 附件:关于求y=kx+b的相关公式
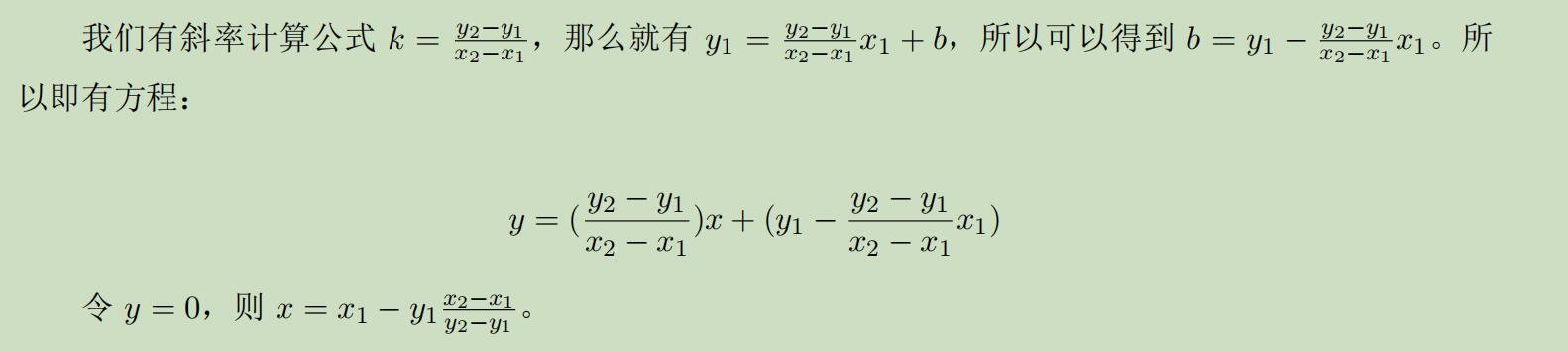
- 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
using namespace std;
ll sc() {
ll xx=0,ff=1; char cch=gc;
while(cch<'0'|| cch>'9') {
if(cch=='-') ff=-ff; cch=gc;
}
while(cch>='0'&& cch<='9') {
xx=(xx<<1)+(xx<<3)+(cch^48); cch=gc;
}
return xx*ff;
}
ll n,cnt;
ll lax,lay,x,y;
ll ans[Maxn];
int main() {
n=sc();
lax=sc(); lay=sc(); //lax lay 为上一个点的横纵坐标
if(!lay)
ans[++cnt]=lax; //如果第一个点的纵坐标为0,则lax为一个零点
for(ll i=2; i<=n; i++) {
x=sc(); y=sc();
if(i==2&& ((lay>0&&y>lay&&(y-lay)*(x-lax)>0)|| (lay<0&&y<lay&&(y-lay)*(x-lax)<0))) //处理射线,当射线满足形似'/'或'\'时
if((lay*(x-lax)%(y-lay))==0) { //零点为整点
ans[++cnt]=lax-lay*(x-lax)/(y-lay); //由公式求出零点
if(cnt>Maxx) {
printf("-1\n");
return 0;
}
}
if(lay==0&&y==0) { //如果当前点和上一点在x轴上
if(i==2||i==n) { //如果在射线上,那么数量肯定会超过3e5
printf("-1\n");
return 0;
}
for(ll j=lax+1; j<=x; j++) { //否则就把它们之间的零点存入
ans[++cnt]=j;
if(cnt>Maxx) {
printf("-1\n");
return 0;
}
}
}
else if(lay!=0&&y==0) { //如果上一点不在x轴上,而当前点在x轴上,存入
ans[++cnt]=x;
if(cnt>Maxx) {
printf("-1\n");
return 0;
}
}
else if(lay*y<0) { //如果前后两点在x轴两侧
if((lay*(x-lax)%(y-lay))==0) { //同上
ans[++cnt]=lax-lay*(x-lax)/(y-lay);
if(cnt>Maxx) {
printf("-1\n");
return 0;
}
}
}
if(i==n&& ((y<0&&y>lay&&(y-lay)*(x-lax)>0)|| (y>0&&y<lay&&(y-lay)*(x-lax)<0))) //处理第二条射线,思路和第一条射线基本一样,但做法不同
if((lay*(x-lax)%(y-lay))==0) {
ans[++cnt]=lax-lay*(x-lax)/(y-lay);
if(cnt>Maxx) {
printf("-1\n");
return 0;
}
}
lax=x; lay=y; //更新上一个点坐标
}
printf("%lld\n",cnt); //输出
for(ll i=1; i<=cnt; i++)
printf("%lld ",ans[i]);
return 0;
}