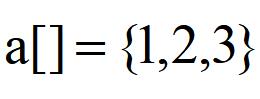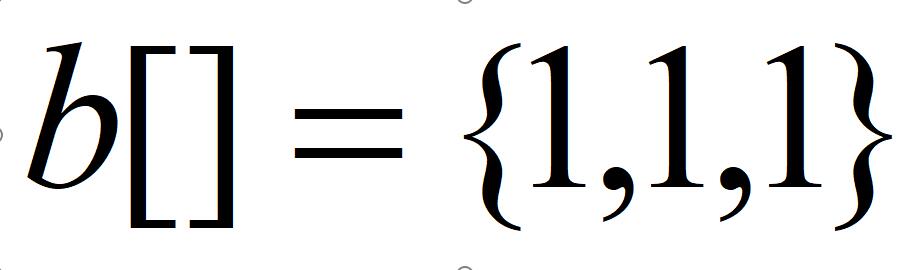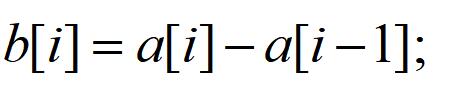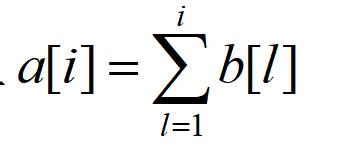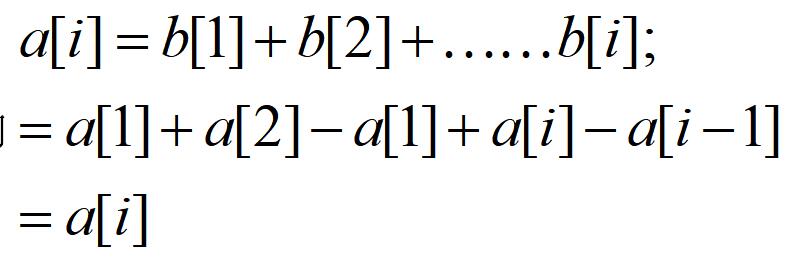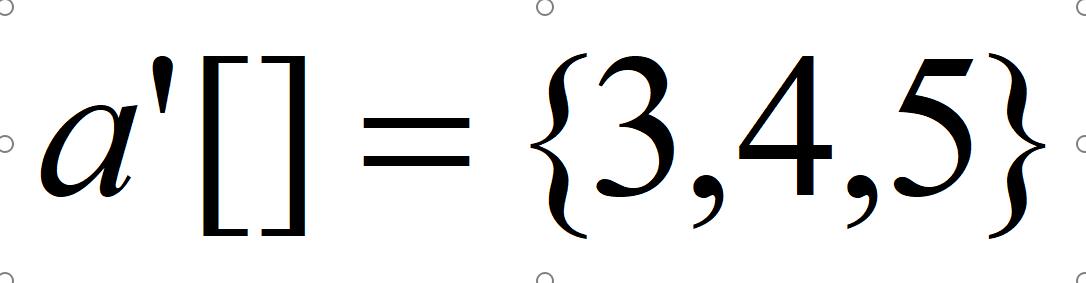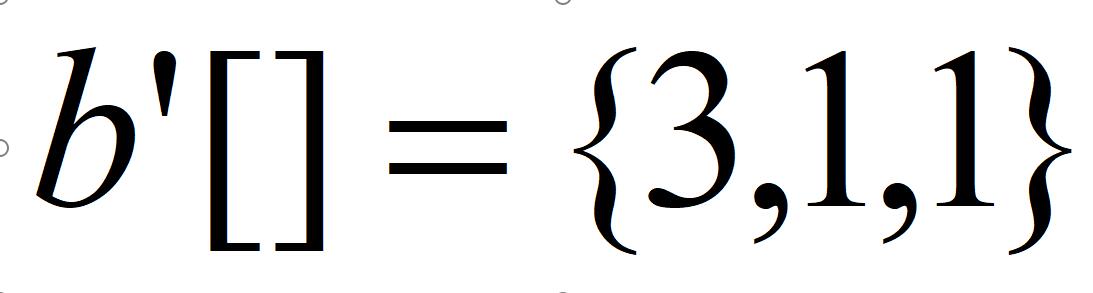模板_树状数组2

题目链接：【模板】树状数组 2
题目思路：基本的树状数组操作就不讲了，讲一下对于本题的差分思路。
- 差分：
  原数组
  
  差分数组
  
  即为
  
  我们可以得出
  
  即
  
  如果我们把原数组都加上2，即变为
  
  差分数组变为
  
  因为a[i]-a[i-1]是不变的，变得只有b[1]和b[3 + 1] (在这个样例中后者可以省略)
  所以对a[x,y]进行修改,只用修改b[x]与b[y+1]
- 对于本题，我们可以把原数组记录下来，在用树状数组维护差分数组（即在原数基础上的变化），输出原数组加上变化值即可。

代码

#include<iostream>
#include<cstdio>
using namespace std;
int n, m;
int a[500010], b[500010];
int qwery(int x) {
    int sum = 0;
    while(x > 0)
    {
        sum += a[x];
        x -= ( x & -x);
    }
    return sum;
}
void updata(int x,int i) {
    while( x <= n)
    {
        a[x] += i;
        x += (x & -x);
    }
}
int main() {
    scanf("%d%d", &n, &m); 
    for(int i = 1 ;i <= n; i++)
        scanf("%d", &b[i]);
    for(int i=1;i<=m;i++) {
        char c;
        cin >> c;
        if(c == '1') {
            int x, y, k;
            scanf("%d%d%d", &x, &y, &k);
            updata(x, k);
            updata(y + 1, -k);
        }
        if(c=='2') {
            int x;
            scanf("%d", &x);
            printf("%d\n", b[x] + qwery(x));
        } 
    }
    return 0;
}

差分：

rp++