mst(欧拉函数)

题面

题目思路：根据题意，我们可以和jmy一样一眼看出最小生成树的边权和，因为每条边的边权为gcd(i,j)，如果两个数互质，即gcd(i,j)=1，则边权为最小，所以MST的边权和为n-1（即每条边边权都为1），那么怎样求MST的个数呢？

我们假设已经枚举到了第i个点，与i互质的点有k个，那么根据乘法原理，总方案数要乘上k，所以这个题目可以转换成从第2个点到第n个点比小于等于它且与它互质的数目的乘积。
这时，我们要用到一个数论知识：

欧拉函数

欧拉函数写作φ(x)（φ读作fài）,表示比不大于x且与x互质的数的数目，这个函数有一些性质：

1.φ(1)= 1
2.φ(x)= x-1（x为质数，与x互质的数即为1到x-1，所以数目为x-1）
3.φ(p^k)=p^k-p^(k-1) （我们知道比p^k小的正整数有p^k - 1个，其中不与p互质的数有p^(k-1)-1 个，它们是 1p,2p,3p … ( p ^ (k-1)-1) p，所以φ(p^k) = (p^k-1) - (p^(k-1)-1) = p^k - p^(k-1) = p^k-p^(k-1) ）
4.我们可以把3.中的式子变一下型，提出一个p^k来，就变成了(p^k)*(1-1/p)
5.欧拉函数为积性函数，对于本函数来说，性质如下图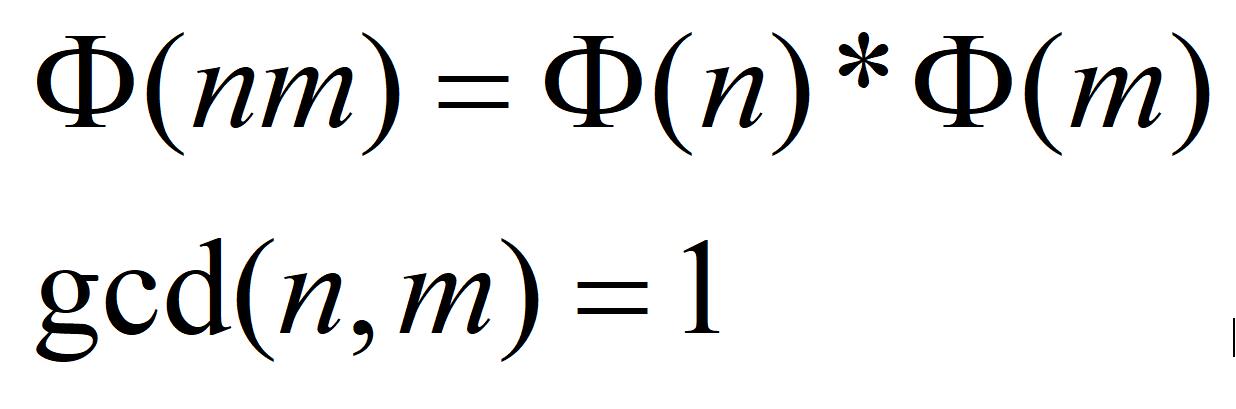具体证明方法请自行查阅。
6.更进一步，请看下图（转自shl）

7.我们可以通过线性筛来求欧拉函数，更确切的说，线性筛可以求出任何一个积性函数。

 1
线性筛：为埃拉托色尼筛法的进阶版，时间复杂度为O(n)，可以保证每个数只被筛一次，具体代码及解释如下

for(int i = 2; i <= n; i++) { //从2开始枚举 
if(! pd[i]) a[++cnt] = i; //如果当前数为质数，加到a数组中 
for(int j = 1; j <= cnt && i * a[j] <= n; j++) { 
pd[i * a[j]] = 1; //标记合数 
if(i % a[j] == 0) break; //重点！如果i % a[j] == 0，说明a[j]为i的最小因数，如果继续循环，则a[j+1]可能等于a[i]*一个未知数，这样就不能保证每个数只判断一次 
	}
}

8.0 我们再来说一下如何用线性筛求欧拉函数，因为欧拉函数为积性函数，如果i mod p != 0, 那么 φ(i p) = φ(i) φ(p)，如果 i mod p == 0, 那么 φ(i p) == p φ(i)。我们这样就AC了
8.1 关于i mod p == 0, 那么 φ(i p) == p φ(i) 的证明，见下图

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define gc getchar()
#define ll long long
#define Maxn 20010
#define mod 100000007
using namespace std;
int sc() {
	int xx = 0, ff = 1; char cch = gc;
	while (cch < '0' || cch > '9') {
		if (cch == '-') ff = -1; cch = gc;
	}
	while (cch >= '0'&& cch <= '9') {
		xx = (xx << 1) + (xx << 3) + (cch ^ '0'); cch = gc;
	}
	return xx * ff;
}
int n, cnt;
int a[Maxn], f[Maxn];
bool pd[Maxn];
ll ans = 1;
int main() {
	freopen("mst.in", "r", stdin);
	freopen("mst.out", "w", stdout);
	n = sc();
	f[1] = 1;
	pd[1] = 1;
	for(int i = 2; i <= n; i++) {
		if(! pd[i]) {
			a[++cnt] = i;
			f[i] = i - 1;
		}
		for(int j = 1; j <= cnt && i * a[j] <= n; j++) {
			pd[i * a[j]] = 1;
			if(! (i % a[j])) {
				f[i * a[j]] = f[i] * (f[a[j]] + 1);
				break;
			}
			else
				f[i * a[j]] = f[i] * f[a[j]];
		}
	}
//	for(int i = 1; i <= n; i++)
//		printf("%d ", f[i]);
//	printf("\n");
	for(int i = 2; i <= n; i++)
		ans = (ans * f[i] % mod) % mod;
	printf("%lld\n", ans % mod);
	return 0;
}

欧拉函数

欧拉函数写作φ(x)（φ读作fài）,表示比不大于x且与x互质的数的数目， 这个函数有一些性质：

rp++

欧拉函数写作φ(x)（φ读作fài）,表示比不大于x且与x互质的数的数目，这个函数有一些性质：