exgcd及逆元

发表于 更新于 分类于
  • 相关题目链接：

同余方程

模板_乘法逆元

  • 题目相关内容：数论之exgcd以及线性递推求逆元。

  • exgcd

    基本模型，形如ax+by=c的方程，要是方程有整数解，我们可得c=gcd(a,b)，我们可以用exgcd求出其最小整数解，我们已知a,b，当b=0是，显然得a=1，我们考虑一下gcd的过程，加入当前我们已求得bx2+a%by2=gcd(a,b)的解为x2,y2,那如何得出x1,y1呢？具体证明过程请见下图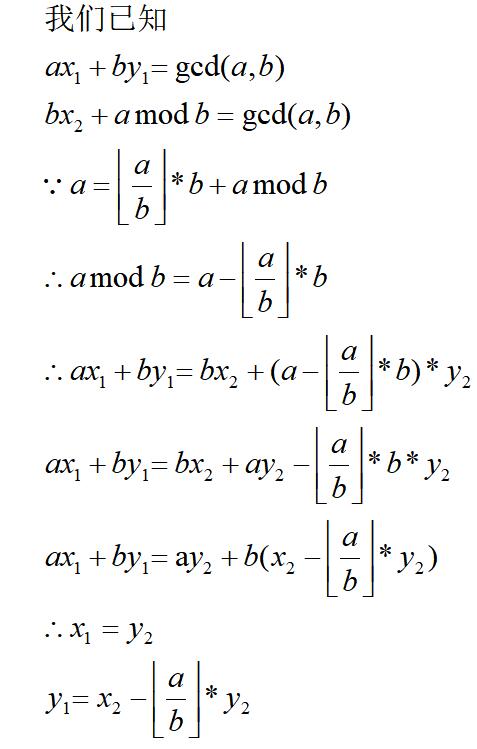
    exgcd的时间复杂度与gcd类似，最坏情况下为θ(nlogn)

  • exgcd求逆元

    逆元：求关于x的同余方程 ax≡1(mod b) 的最小正整数解，x即为a的逆元。
    根据裴蜀定理，要使同余方程ax≡1(mod b)有解，要满足gcd(a,p)|b，由题意得，b=1，所以gcd(a,p)=1
    我们再来分析一下这个同余方程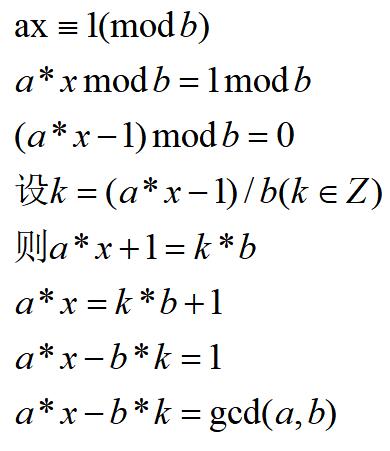
    所以，我们可以通过exgcd来解这个方程，同时这也求出了a的逆元。

  • 代码（T1 AC）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    #include<iostream>
    #include<cstdio>
    #include<cstring>
    #include<algorithm>
    #define gc getchar()
    #define ll long long
    using namespace std;
    ll sc() {
    	ll xx = 0, ff = 1; char cch = gc;
    	while (cch < '0' || cch > '9') {
    		if (cch == '-') ff = -1; cch = gc;
    	}
    	while (cch >= '0'&& cch <= '9') {
    		xx = (xx << 1) + (xx << 3) + (cch ^ '0'); cch = gc;
    	}
    	return xx * ff;
    }
    ll n, m;
    ll exgcd(ll a, ll b, ll &x, ll &y) {
    	if(!b) {
    		x = 1;
    		y = 0;
    		return a;
    	}
    	ll gcd = exgcd(b, a % b, x, y);
    	ll x2 = x, y2 = y;
    	x = y2;
    	y = x2 - a / b * y2;
    	return gcd;
    }
    int main() {
    	ll x = 0, y = 0;
    	n = sc(); m = sc();
    	exgcd(n, m, x, y);
    	printf("%lld\n", (x + m) % m);
    	return 0;
    }

  • 代码（T2 80Pts）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    #include<iostream>
    #include<cstdio>
    #include<cstring>
    #include<algorithm>
    #define gc getchar()
    #define ll long long
    using namespace std;
    ll sc() {
    	ll xx = 0, ff = 1; char cch = gc;
    	while (cch < '0' || cch > '9') {
    		if (cch == '-') ff = -1; cch = gc;
    	}
    	while (cch >= '0'&& cch <= '9') {
    		xx = (xx << 1) + (xx << 3) + (cch ^ '0'); cch = gc;
    	}
    	return xx * ff;
    }
    ll n, m;
    ll exgcd(ll a, ll b, ll &x, ll &y) {
    	if(!b) {
    		x = 1;
    		y = 0;
    		return a;
    	}
    	ll gcd = exgcd(b, a % b, x, y);
    	ll x2 = x, y2 = y;
    	x = y2;
    	y = x2 - a / b * y2;
    	return gcd;
    }
    int main() {
    	ll x = 0, y = 0;
    	n = sc(); m = sc();
    	for(int i = 1; i <= n; i++) {
    		x = 0, y = 0;
    		exgcd(i, m, x, y);
    		printf("%lld\n", (x + m) % m);
    	}
    	return 0;
    }

  • 线性递推求逆元

    首先，我们声明在下列计算中同余均是在mod p意义下

    我们可以简单计算1^(-1)≡1

    考虑任意正整数i，假定i-1的逆元已经正确计算，我们递推方程的计算过程如下：

  • 代码（T2 AC）
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    #include<iostream>
    #include<cstdio>
    #include<cstring>
    #include<algorithm>
    #define gc getchar()
    #define ll long long
    #define Maxn 3000010
    using namespace std;
    ll sc() {
    	ll xx = 0, ff = 1; char cch = gc;
    	while (cch < '0' || cch > '9') {
    		if (cch == '-') ff = -1; cch = gc;
    	}
    	while (cch >= '0'&& cch <= '9') {
    		xx = (xx << 1) + (xx << 3) + (cch ^ '0'); cch = gc;
    	}
    	return xx * ff;
    }
    ll n, m;
    ll f[Maxn];
    int main() {
    	n = sc(); m = sc();
    	f[1] = 1;
    	for(int i = 2; i <= n; i++)
    		f[i] = (m - m / i) * f[m % i] % m;
    	for(int i = 1; i <= n; i++)
    		printf("%lld\n", f[i]);
    	return 0;
    }
rp++