紧急集合|聚会

发表于 更新于 分类于

Problem’s Website

  • 紧急集合 / 聚会

    Solution

  • 这是一道求树上三点的最短距离题，我们知道，树上两点的最短距离为两点到两点的LCA的距离之和，那么三个点的最短距离如何求呢？
  • 肯定也和LCA有关，假设我们现在有a,b,c三个点，aa = LCA(a, b),bb = LCA(b, c),cc = LCA(c, a),结论是：aa,bb,cc中不同与其他两点的点为最短路径的必经之点，至于证明，本蒟蒻不太会，胡乱证明一下，见下图：

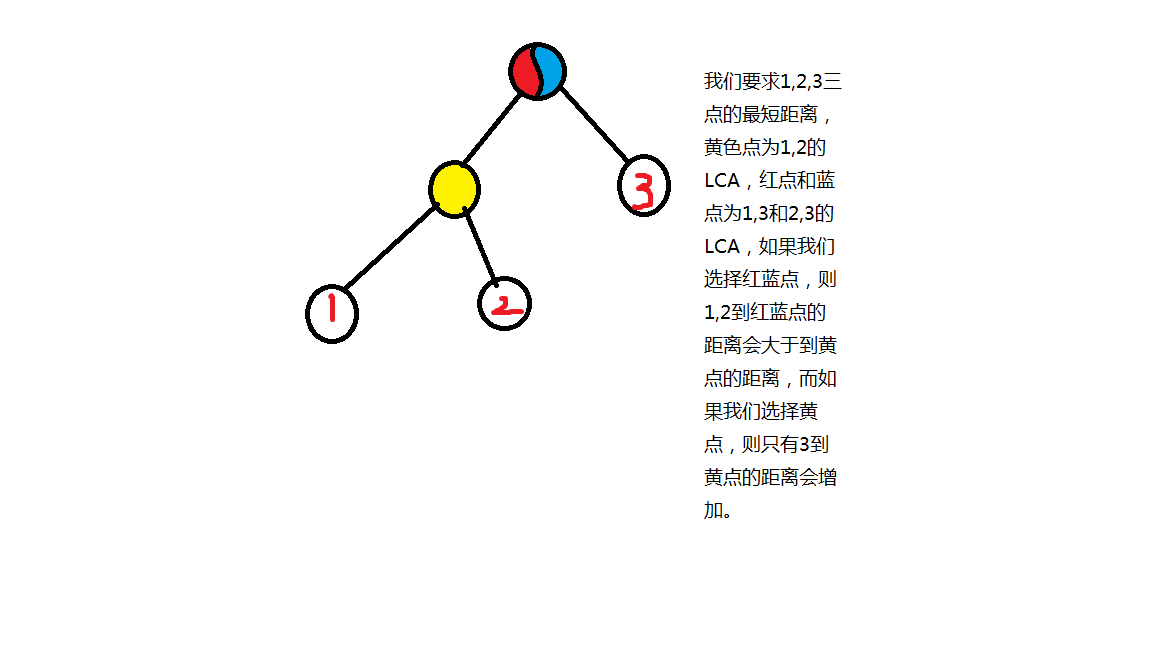
    Code

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    #include<iostream>
    #include<cstdio>
    #include<cstring>
    #include<algorithm>
    #define gc getchar()
    #define Maxn 500010
    using namespace std;
    int sc() {
    	int xx=0,ff=1; char cch;
    	while(cch<'0'|| cch>'9') {
    		if(cch=='-') ff=-ff; cch=gc;
    	}
    	while(cch>='0'&& cch<='9') {
    		xx=xx*10+(cch-48); cch=gc;
    	}
    	return xx*ff;
    }
    struct TREE {
    	int next,to;
    }edge[Maxn*2];
    int cnt,n,m;
    int head[Maxn*2],deep[Maxn];
    int f[Maxn][21];
    namespace DY {
    	void ADD(int from,int to) {
    		edge[++cnt].next=head[from];
    		edge[cnt].to=to;
    		head[from]=cnt;
    	}
    	void D_F(int son,int fa) {
    		deep[son]=deep[fa]+1;
    		for(int i=1; i<=19; i++)
    			f[son][i]=f[f[son][i-1]][i-1];
    		for(int i=head[son]; i; i=edge[i].next) {
    			int to=edge[i].to;
    			if(to==fa) continue;
    			f[to][0]=son;
    			D_F(to,son);
    		}
    	}
    	int LCA(int x,int y) {
    		if(deep[x]<deep[y]) swap(x,y);
    		for(int i=20; i>=0; i--) {
    			if(deep[f[x][i]]>=deep[y])
    				x=f[x][i];
    			if(x==y) return x;
    		}
    		for(int i=20; i>=0; i--) {
    			if(f[x][i]!=f[y][i])
    				x=f[x][i],y=f[y][i];
    		}
    		return f[x][0];
    	}
    	void main() {
    		n=sc(); m=sc();
    		for(int i=1; i<n; i++) {
    			int u=sc(),v=sc();
    			ADD(u,v); ADD(v,u);
    		}
    		D_F(1,0);
    		while(m--) {
    			int aa=sc(),bb=sc(),cc=sc(),d1;
    			int a1=LCA(aa,bb);
    			int b1=LCA(aa,cc);
    			int c1=LCA(bb,cc);
    			if(a1==b1) d1=c1;
    			else if(a1==c1) d1=b1;
    			else if(b1==c1) d1=a1;
    			int res=deep[aa]+deep[bb]+deep[cc]-deep[a1]-deep[b1]-deep[c1];
    			printf("%d %d\n",d1,res);
    		}
    	}
    };
    int main() {
    	DY::main();
    	return 0;
    }

rp++