ST表模板

发表于 更新于 分类于

Problem’s Website

  • 模板_ST表

    Solution

  • ST表是一种利用倍增实现快速查找区间内极值的黑科技，但一般的ST表都是静态的，本菜鸡不会动态修改。。。

  • 我们设$st[i][j]$为从第$i$个位置开始，长度为$2^j$中的极值，那怎样处理呢？代码为(以取最大值为例)

    1
    2
    st[i][0] = a[i];
    st[i][j] = max(st[i][j - 1],  st[i + (1 << (j - 1))][j - 1]);

    第二行的大家可能不太懂，我画个图解释一下

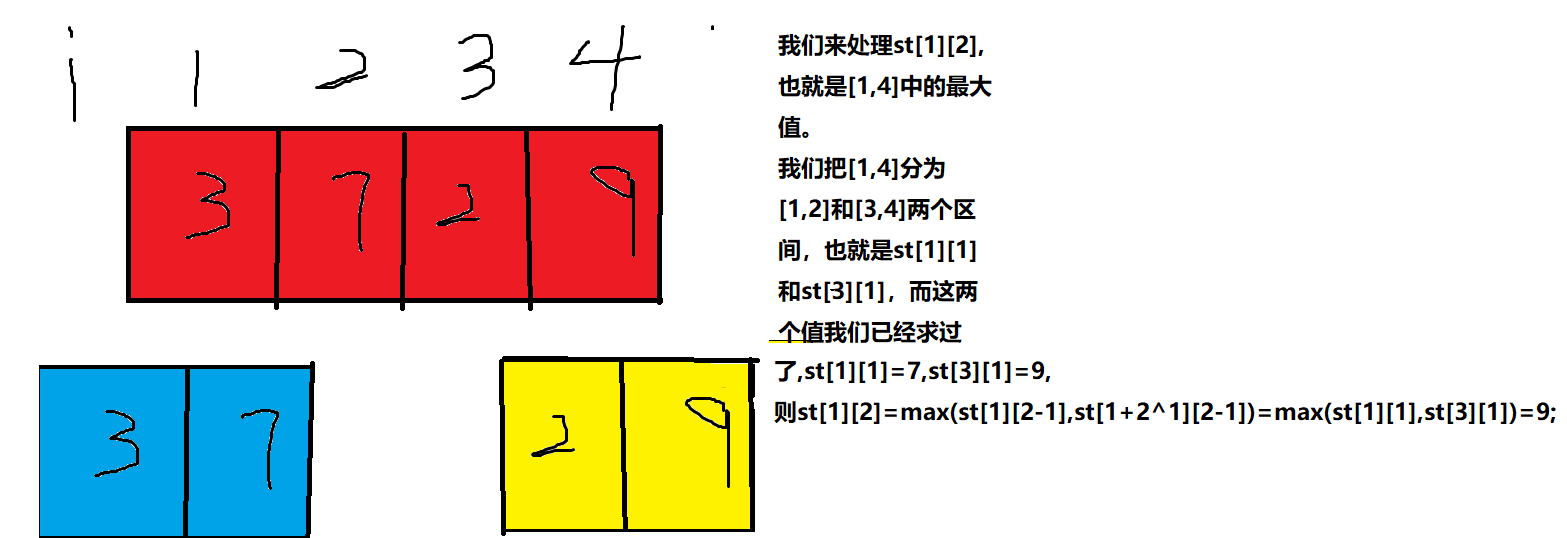
  • 那怎样区间求极值呢？假设区间为$[x,y]$代码为

    1
    2
    int p = (int)log2(y - x + 1);
    ans = max(st[x][p], st[y - (1 << p) + 1][p]);

    我再来画个图来解释一下

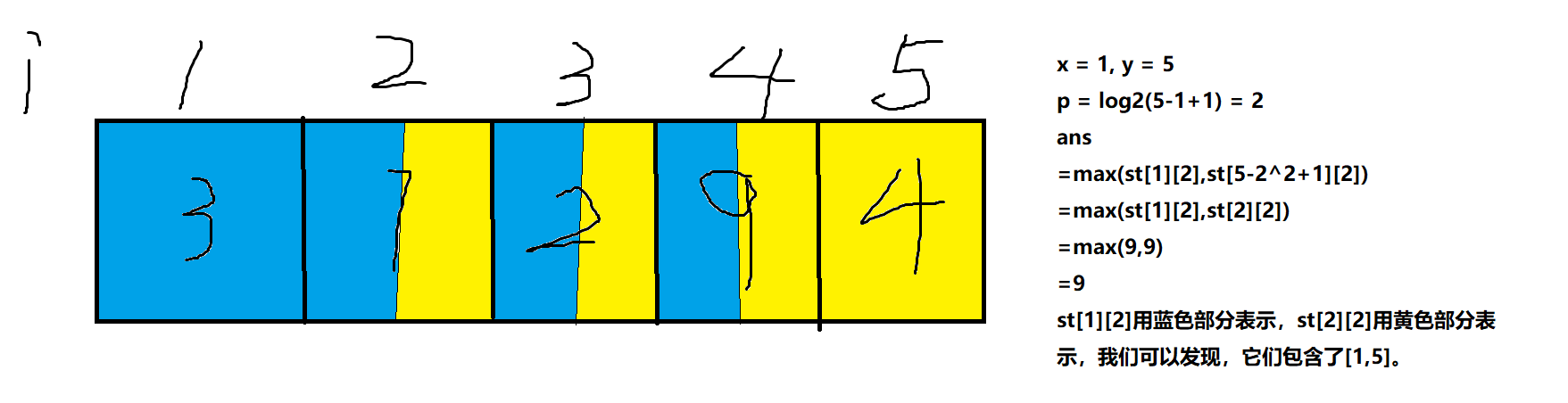
    Code

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    #include<iostream>
    #include<cstdio>
    #include<cstring>
    #include<algorithm>
    #include<cmath>
    #define gc getchar()
    #define pc(x) putchar(x)
    #define re register
    const int Maxn = 100010;
    inline int sc() {
        int xx = 0, ff = 1; char cch = gc;
        while(!isdigit(cch)) {
            if(cch == '-') ff = -1; cch = gc;
        }
        while(isdigit(cch)) {
            xx = (xx << 1) + (xx << 3) + (cch ^ '0'); cch = gc;
        }
        return xx * ff;
    }
    inline void out(int x) {
        if(x < 0) pc('-'), x = -x;
        if(x >= 10)
            out(x / 10);
        pc(x % 10 + '0');
    }
    int n, m;
    int st[Maxn][20];
    int main() {
    	n = sc(), m = sc();
    	for(re int i = 1; i <= n; ++i)
    		st[i][0] = sc();
    	int lim = (int)log2(n);
    //	std :: cerr << lim << std :: endl;
    	for(re int j = 1; j <= lim; ++j)
    		for(re int i = 1; i <= n - (1 << j) + 1; ++i)
    			st[i][j] = std :: max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
    	for(re int i = 1; i <= m; ++i) {
    		int x = sc(), y = sc();
    		int p = (int)log2(y - x + 1);
    		out(std :: max(st[x][p], st[y - (1 << p) + 1][p])), pc('\n');
    	}
        return 0;
    }
    // Coded by dy.

rp++