浅谈树链剖分

发表于 更新于 分类于

Problem’s Website

  • 模板_树链剖分
  • ZHOI2008_树的统计

    Solution

  • 树链剖分前置知识：
    • 线段树
    • 树的dfs遍历
  • 以上内容不会的同学可以先去学习一下，特别是线段树，我的其他几篇Blog有对其的介绍。

  • So，树链剖分到底是啥？

  • 一句话：在树上做线段树。

  • 首先，我们知道，对一棵树进行dfs遍历，记录每一个点的dfs序，这样就可以把一棵树转化成一个序列，但既然叫树链剖分，肯定不能就这样简单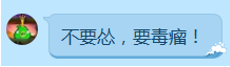，,我们要通过一些规则将树分成若干条链，那为什么要分链呢？直接对整棵树dfs遍历不就行了吗？

  • 一开始我就说了，这种做法的正确性肯定是对的，但我们看下图：

    ，如果对这棵树进行dfs遍历，会用很多时间，如果对一些数据很大题目，很可能就T飞了。。。

  • 所以，我们要分链，目的就是为了降低时间复杂度，那怎样分可以降低呢？很简单，对于一个节点，选择其子树最多的节点。

  • 接下来，我们来说一些专有名词

    • 重儿子：父亲节点的所有儿子中子树结点数目最多的结点；

    • 轻儿子：父亲节点中除了重儿子以外的儿子；

    • 重边：父亲结点和重儿子连成的边；

    • 轻边：父亲节点和轻儿子连成的边；

    • 重链：由多条重边连接而成的路径；

    • 轻链：由多条轻边连接而成的路径.
      画个图来演示一下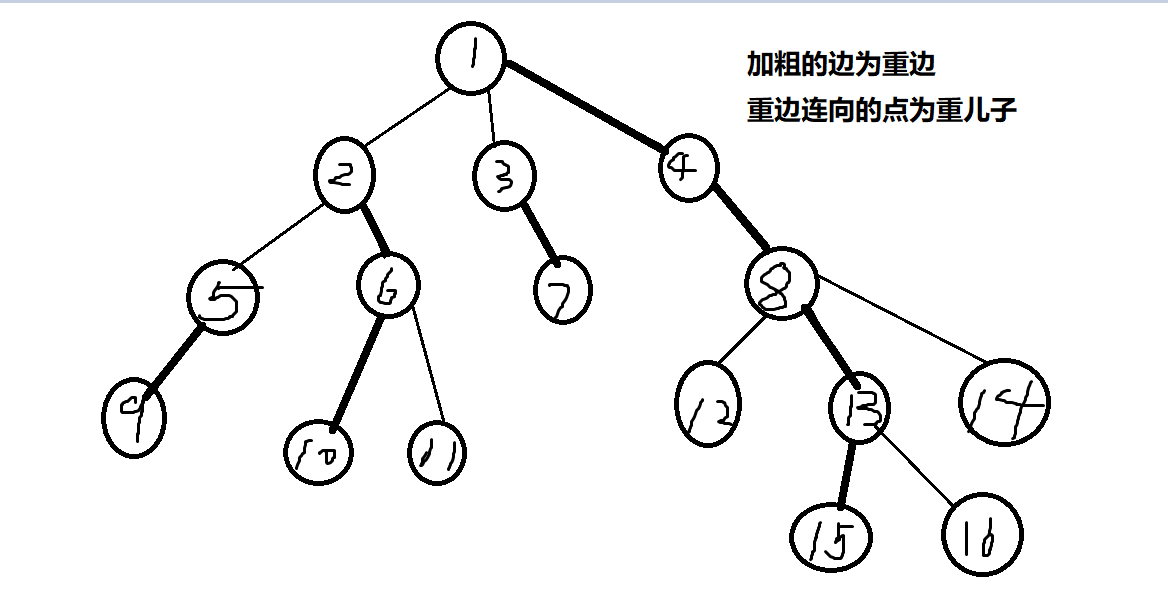
      我们遍历时，沿着重链进行dfs遍历，上图遍历的顺序见下图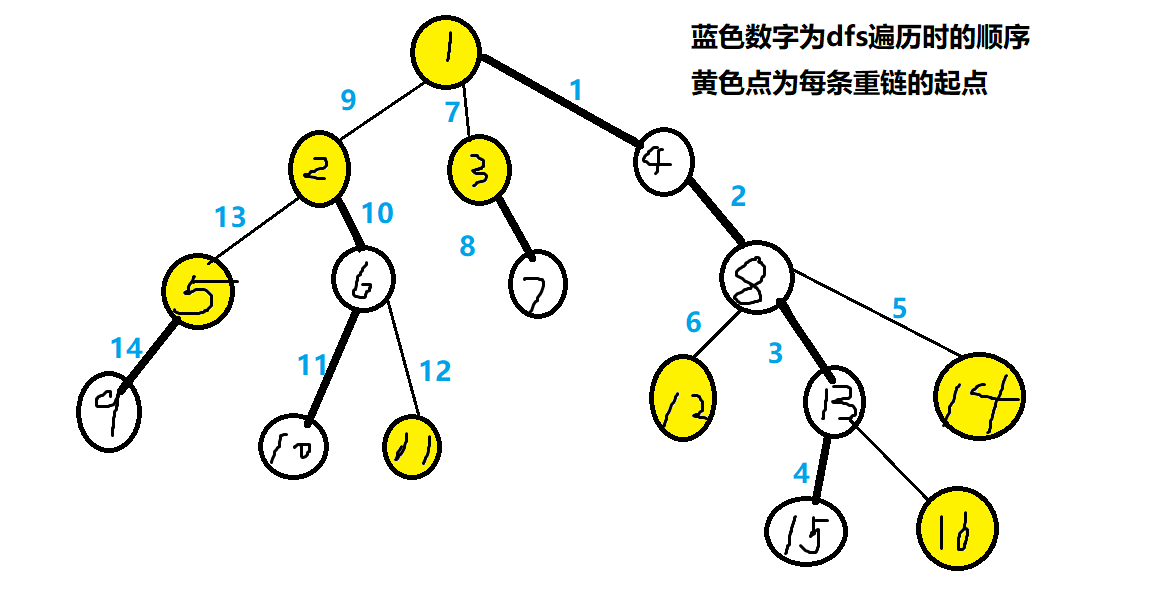

  • 我们再来详细说明一下树链剖分的过程：

    • 首先进行第一次dfs，要求出每个点的深度（dep）、子树大小(siz)、父节点(fa)，和重儿子(son)

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      inline void dfs1(int now, int Fa, int Dep) {
      	dep[now] = Dep;
      	siz[now] = 1;
      	fa[now] = Fa;
      	int Maxson = -1;
      	for(re int i = head[now]; i; i = t[i].next) {
      		int to = t[i].to;
      		if(to == Fa) continue;
      		dfs1(to, now, Dep + 1);
      		siz[now] += siz[to];
      		if(Maxson < siz[to])
      			son[now] = to, Maxson = siz[to];
      	}
      }

    • 然后进行第二次dfs，求出按照上文提到的规则进行遍历，求出每个点的dfs序(id)、dfs序代表的节点(aa)、每条重链的起点(top)

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
         inline void dfs2(int now, int topf) {
      	id[now] = ++cnt;
      	aa[cnt] = a[now];
      	top[now] = topf;
      	if(!son[now]) return;
      	dfs2(son[now], topf);
      	for(re int i = head[now]; i; i = t[i].next) {
      		int to = t[i].to;
      		if(to == fa[now] || to == son[now]) continue;
      		dfs2(to, to);
      	}
      }

    • 这样我们就可以按照dfs序建立线段树，并对其进行维护了！

  • 最后我们介绍一些比较常见的树链剖分操作

    • 下面代码变量的含义在上文，请自行查看。

    • 将树从x到y结点最短路径上所有节点的值都加上z:
      首先这两个点有很大可能不在同一条重链上，那我们就让其中深度大的点往上跳到重链的起点，顺便维护该条重链的线段树，最后两个点在同一条重链上，就维护那条链的线段树即可。

      1
      2
      3
      4
      5
      6
      7
      8
      9
            inline void upxy(int x, int y, int z) {
       while(top[x] != top[y]) {
      	 if(dep[top[x]] < dep[top[y]]) std :: swap(x, y);
      	 modify(1, 1, n, id[top[x]], id[x], z);
      	 x = fa[top[x]];
       }
       if(dep[x] > dep[y]) std :: swap(x, y);
       modify(1, 1, n, id[x], id[y], z);
      }

      • 求树从x到y结点最短路径上所有节点的值之和\最大值：
        类似于上文，两个点如果不在一条重链，就让其中一个点往上跳，顺便记录信息，最后在一条链上，记录信息。(下面代码为维护区间和，维护区间最大值见下文CodeT2)

        1
        2
        3
        4
        5
        6
        7
        8
        9
        10
        11
              inline int qyxy(int x, int y) {
        	int res = 0;
        	while(top[x] != top[y]) {
        			if(dep[top[x]] < dep[top[y]]) std :: swap(x, y);
        			res = (res + query(1, 1, n, id[top[x]], id[x])) % p;
        			x = fa[top[x]];
        	}
        	if(dep[x] > dep[y]) std :: swap(x, y);
        	res = (res + query(1, 1, n, id[x], id[y])) % p;
        	return res;
        }

      • 将以x为根节点的子树内所有节点值都加上z：
        我们计算可得，一棵子树的右节点为当前节点的dfs序号+子树大小-1，那我们就线段树区间修改即可。

        1
        2
        3
              inline void upx(int x, int z) {
        	modify(1, 1, n, id[x], id[x] + siz[x] - 1, z);
        }

      • 求以x为根节点的子树内所有节点值之和：
        类似于上文，用线段树区间查询即可。

        1
        2
        3
              inline int qyx(int x) {
        	return query(1, 1, n, id[x], id[x] + siz[x] - 1) % p;
        }

  • 讲到这里，两道题目其实已经解决了，下面是整理后的代码。

2019.8.2 Update:

关于树链剖分的一些性质和其时间复杂度证明。（以下内容来自一本通提高版，由我读后，根据理解自己撰写的）

一些性质：

1.如果$(u,v)$为轻边，则$siz[v] \le siz[u] /2$

证明：反证法，如果$siz[v] > siz[u]$,则$siz[v]$要比其他儿子的子树大小要大，那么$(u,v)$必不可能为轻边。

2.从根节点到某一点$node$的路径上的轻边个数不超过$log n$.

证明：根据轻重边的定义，我们可知，当$node$为叶子节点时，轻边的数量最多，有性质$1$可知，每经过一条轻边，子树大小就会比原来少一半，所以至少有$log n$条轻边。

约定：下文中所出现的重路径即为重链（特别地，一个叶子节点也算一条重路径）。

3.对于每个点，从它到根节点的路径上都有不超过$log n$条轻边和$log n$条重路径。

证明：显然每条重路径的起点和终点都是由轻边构成，由性质$2$可知，每个点到根节点的轻边数量为$log n$，所以重路径数量也为$log n$。

树链剖分的时间复杂度及其证明：

对一棵树进行分链后，对于路径$(u,v)$,我们可以分别处理$u,v$两点到其$LCA$的路径，根据性质$3$，路径最多分解成$log n$条重路径和$log n$条轻边，对于重路径，我们可以用一棵线段树来维护，对于轻边，我们直接跳过，访问下一条重路径，因为轻边的两端点一定在两条重路径上，这两种操作的时间复杂度分别为$\Theta(log^2n)$和$\Theta(logn)$，总复杂度为$\Theta(log^2n)$

Code

  • T1

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    92
    93
    94
    95
    96
    97
    98
    99
    100
    101
    102
    103
    104
    105
    106
    107
    108
    109
    110
    111
    112
    113
    114
    115
    116
    117
    118
    119
    120
    121
    122
    123
    124
    125
    126
    127
    128
    129
    130
    131
    132
    133
    134
    135
    136
    137
    138
    139
    140
    141
    142
    143
    144
    145
    146
    147
    148
    149
    150
    151
    152
    153
    154
    155
    156
    157
    158
    159
    160
    161
    162
    163
    164
    #include<iostream>
    #include<cstdio>
    #include<cstring>
    #include<algorithm>
    #define gc getchar()
    #define pc(x) putchar(x)
    #define re register
    const int Maxn = 1e5 + 10;
    inline int sc() {
    	int xx = 0, ff = 1; char cch = gc;
    	while(!isdigit(cch)) {
    		if(cch == '-') ff = -1; cch = gc;
    	}
    	while(isdigit(cch)) {
    		xx = (xx << 1) + (xx << 3) + (cch ^ '0'); cch = gc;
    	}
    	return xx * ff;
    }
    inline void out(int x) {
    	if(x >= 10)
    		out(x / 10);
    	pc(x % 10 + '0');
    }
    struct node {
    	int next, to;
    }t[Maxn << 1];
    struct LST {
    	int data, tag;
    }lst[Maxn << 2];
    int n, m, s, p, cnt;
    int a[Maxn], head[Maxn];
    int id[Maxn], top[Maxn], son[Maxn], siz[Maxn], aa[Maxn], dep[Maxn], fa[Maxn];
    inline void ADD(int from, int to) {
    	t[++cnt].next = head[from];
    	t[cnt].to = to;
    	head[from] = cnt;
    }
    inline void build(int k, int l, int r) {
    	if(l == r) {
    		lst[k].data = aa[l];
    		if(lst[k].data > p) lst[k].data %= p;
    		return;
    	}
    	int mid = l + r >> 1;
    	build(k << 1, l, mid), build(k << 1 | 1, mid + 1, r);
    	lst[k].data = (lst[k << 1].data + lst[k << 1 | 1].data) % p;
    }
    inline void pushdown(int k, int l, int r) {
    	if(!lst[k].tag) return;
    	lst[k << 1].tag += lst[k].tag;
    	lst[k << 1 | 1].tag += lst[k].tag;
    	int len = r - l + 1;
    	lst[k << 1].data = (lst[k << 1].data + lst[k].tag * (len - (len >> 1))) % p;
    	lst[k << 1 | 1].data = (lst[k << 1 | 1].data + lst[k].tag * (len >> 1)) % p;
    	lst[k].tag = 0;
    }
    inline void modify(int k, int l, int r, int x, int y, int z) {
    	if(x <= l && r <= y) {
    		lst[k].tag += z;
    		lst[k].data = (lst[k].data + z * (r - l + 1)) % p;
    		return;
    	}
    	int mid = l + r >> 1;
    	pushdown(k, l, r);
    	if(x <= mid) modify(k << 1, l, mid, x, y, z);
    	if(y > mid) modify(k << 1 | 1, mid + 1, r, x, y, z);
    	lst[k].data = (lst[k << 1].data + lst[k << 1 | 1].data) % p;
    }
    inline int query(int k, int l, int r, int x, int y) {
    	if(x <= l && r <= y) {
    		return lst[k].data % p;
    	}
    	int res = 0, mid = l + r >> 1;
    	pushdown(k, l, r);
    	if(x <= mid) res = (res + query(k << 1, l, mid, x, y)) % p;
    	if(y > mid) res = (res + query(k << 1 | 1, mid + 1, r, x, y)) % p;
    	return res % p;
    }
    inline void upxy(int x, int y, int z) {
    	z %= p;
    	while(top[x] != top[y]) {
    		if(dep[top[x]] < dep[top[y]]) std :: swap(x, y);
    		modify(1, 1, n, id[top[x]], id[x], z);
    		x = fa[top[x]];
    	}
    	if(dep[x] > dep[y]) std :: swap(x, y);
    	modify(1, 1, n, id[x], id[y], z);
    }
    inline int qyxy(int x, int y) {
    	int res = 0;
    	while(top[x] != top[y]) {
    		if(dep[top[x]] < dep[top[y]]) std :: swap(x, y);
    		res = (res + query(1, 1, n, id[top[x]], id[x])) % p;
    		x = fa[top[x]];
    	}
    	if(dep[x] > dep[y]) std :: swap(x, y);
    	res = (res + query(1, 1, n, id[x], id[y])) % p;
    	return res;
    }
    inline void upx(int x, int z) {
    //	z %= p;
    	modify(1, 1, n, id[x], id[x] + siz[x] - 1, z);
    }
    inline int qyx(int x) {
    	return query(1, 1, n, id[x], id[x] + siz[x] - 1) % p;
    }
    inline void dfs1(int now, int Fa, int Dep) {
    	dep[now] = Dep;
    	siz[now] = 1;
    	fa[now] = Fa;
    	int Maxson = -1;
    	for(re int i = head[now]; i; i = t[i].next) {
    		int to = t[i].to;
    		if(to == Fa) continue;
    		dfs1(to, now, Dep + 1);
    		siz[now] += siz[to];
    		if(Maxson < siz[to])
    			son[now] = to, Maxson = siz[to];
    	}
    }
    inline void dfs2(int now, int topf) {
    	id[now] = ++cnt;
    	aa[cnt] = a[now];
    	top[now] = topf;
    	if(!son[now]) return;
    	dfs2(son[now], topf);
    	for(re int i = head[now]; i; i = t[i].next) {
    		int to = t[i].to;
    		if(to == fa[now] || to == son[now]) continue;
    		dfs2(to, to);
    	}
    }
    int main() {
    	n = sc(), m = sc(), s = sc(), p = sc();	
    	for(re int i = 1; i <= n; ++i)
    		a[i] = sc();
    	for(re int i = 1; i < n; ++i) {
    		int x = sc(), y = sc();
    		ADD(x, y), ADD(y, x);
    	}
    	cnt = 0;
    	dfs1(s, 0, 1), dfs2(s, s), build(1, 1, n);
    	while(m--) {
    		int flag = sc();
    		if(flag == 1) {
    			int x = sc(), y = sc(), z = sc();
    			upxy(x, y, z);
    		}
    		else if(flag == 2) {
    			int x = sc(), y = sc();
    			out(qyxy(x, y)), pc('\n');
    		}
    		else if(flag == 3) {
    			int x = sc(), z = sc();
    			upx(x, z);
    		}
    		else {
    			int x = sc();
    			out(qyx(x)), pc('\n');
    		}
    	}
    	return 0;
    }
    // Coded by dy.

  • T2

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    92
    93
    94
    95
    96
    97
    98
    99
    100
    101
    102
    103
    104
    105
    106
    107
    108
    109
    110
    111
    112
    113
    114
    115
    116
    117
    118
    119
    120
    121
    122
    123
    124
    125
    126
    127
    128
    129
    130
    131
    132
    133
    134
    135
    136
    137
    138
    139
    140
    141
    142
    143
    144
    145
    146
    147
    148
    149
    150
    151
    152
    153
    154
    155
    156
    157
    158
    159
    #include<iostream>
    #include<cstdio>
    #include<cstring>
    #include<algorithm>
    #define gc getchar()
    #define pc(x) putchar(x)
    #define re register
    const int Maxn = 6e4 + 10;
    const int INF = 30000 + 10;
    inline int sc() {
        int xx = 0, ff = 1; char cch = gc;
        while(!isdigit(cch)) {
            if(cch == '-') ff = -1; cch = gc;
        }
        while(isdigit(cch)) {
            xx = (xx << 1) + (xx << 3) + (cch ^ '0'); cch = gc;
        }
        return xx * ff;
    }
    inline void out(int x) {
        if(x < 0) pc('-'), x = -x;
        if(x >= 10)
            out(x / 10);
        pc(x % 10 + '0');
    }
    struct node {
    	int next, to;
    }t[Maxn << 1];
    struct LST {
    	int sum, maxx;
    }lst[Maxn << 2];
    int n, cnt, m;
    int head[Maxn], a[Maxn];
    int id[Maxn], top[Maxn], dep[Maxn], fa[Maxn], aa[Maxn], son[Maxn], siz[Maxn];
    inline void ADD(int from, int to) {
    	t[++cnt].next = head[from];
    	t[cnt].to = to;
    	head[from] = cnt;
    }
    inline void build(int k, int l, int r) {
    	if(l == r) {
    		lst[k].sum = lst[k].maxx = aa[l];
    		return;
    	}
    	int mid = l + r >> 1;
    	build(k << 1, l, mid), build(k << 1 | 1, mid + 1, r);
    	lst[k].maxx = std :: max(lst[k << 1].maxx, lst[k << 1 | 1].maxx);
    	lst[k].sum = lst[k << 1].sum + lst[k << 1 | 1].sum;
    }
    inline void modify(int k, int l, int r, int x, int z) {
    	if(l == r && l == x) {
    		lst[k].sum = lst[k].maxx = z;
    		return ;
    	}
    	int mid = l + r >> 1;
    	if(x <= mid) modify(k << 1, l, mid, x, z);
    	else modify(k << 1 | 1, mid + 1, r, x, z);
    	lst[k].maxx = std :: max(lst[k << 1].maxx, lst[k << 1 | 1].maxx);
    	lst[k].sum = lst[k << 1].sum + lst[k << 1 | 1].sum;
    }
    inline int query_max(int k, int l, int r, int x, int y) {
    	if(x <= l && r <= y) {
    		return lst[k].maxx;
    	}
    	int res = -INF, mid = l + r >> 1;
    	if(x <= mid) res = std :: max(res, query_max(k << 1, l, mid, x, y));
    	if(y > mid) res = std :: max(res, query_max(k << 1 | 1, mid + 1, r, x, y));
    	return res;
    }
    inline int query_sum(int k, int l, int r, int x, int y) {
    	if(x <= l && r <= y) {
    		return lst[k].sum;
    	}
    	int res = 0 , mid = l + r >> 1;
    	if(x <= mid) res += query_sum(k << 1, l, mid, x, y);
    	if(y > mid) res += query_sum(k << 1 | 1, mid + 1, r, x, y);
    	return res;
    }
    inline void update(int x, int z) {
    	modify(1, 1, n, id[x], z);
    }
    inline int qymax(int x, int y) {
    	int res = -INF;
    	while(top[x] != top[y]) {
    		if(dep[top[x]] < dep[top[y]]) std :: swap(x, y);
    		res = std :: max(res, query_max(1, 1, n, id[top[x]], id[x]));
    		x = fa[top[x]];
    	}
    	if(dep[x] > dep[y]) std :: swap(x, y);
    	res = std :: max(res, query_max(1, 1, n, id[x], id[y]));
    	return res;
    }
    inline int qysum(int x, int y) {
    	int res = 0;
    	while(top[x] != top[y]) {
    		if(dep[top[x]] < dep[top[y]]) std :: swap(x, y);
    		res += query_sum(1, 1, n, id[top[x]], id[x]);
    		x = fa[top[x]];
    	}
    	if(dep[x] > dep[y]) std :: swap(x, y);
    	res += query_sum(1, 1, n, id[x], id[y]);
    	return res;
    }
    inline void dfs1(int now, int Fa,int Dep) {
    	dep[now] = Dep;
    	fa[now] = Fa;
    	siz[now] = 1;
    	int Maxson = -1;
    	for(re int i = head[now]; i; i = t[i].next) {
    		int to = t[i].to;
    		if(to == Fa) continue;
    		dfs1(to, now, Dep + 1);
    		siz[now] += siz[to];
    		if(siz[to] > Maxson)
    			Maxson = siz[to], son[now] = to;
    	}
    }
    inline void dfs2(int now, int topf) {
    	top[now] = topf;
    	id[now] = ++cnt;
    	aa[cnt] = a[now];
    	if(!son[now]) return;
    	dfs2(son[now], topf);
    	for(re int i = head[now]; i; i = t[i].next) {
    		int to = t[i].to;
    		if(to == son[now] || to == fa[now]) continue;
    		dfs2(to, to);
    	}
    }
    int main() {
    	n = sc();
    	for(re int i = 1; i < n; ++i) {
    		int x = sc(), y = sc();
    		ADD(x, y), ADD(y, x);
    	}
    	for(re int i = 1; i <= n; ++i)
    		a[i] = sc();
    	cnt = 0;
    	dfs1(1, 0, 1), dfs2(1, 1), build(1, 1, n);
    	m = sc();
    	while(m--) {
    		char c[10];
    		std :: cin >> c;
    		if(c[0] == 'C') {
    			int x = sc(), z = sc();
    			update(x, z);
    		}
    		else if(c[1] == 'M') {
    			int x = sc(), y = sc();
    			out(qymax(x, y)), pc('\n');
    		}
    		else {
    			int x = sc(), y = sc();
    			out(qysum(x, y)), pc('\n');
    		}
    	}
        return 0;
    }
    // Coded by dy.

rp++