SDOI_2014旅行

发表于 更新于 分类于

Problem’s Website

SDOI_2014旅行

Solution

这道题考察了两个知识点，一个是树链剖分，另一个是动态开点线段树。

树剖不会的同学请点击这

我们着重来讲一下动态开点线段树

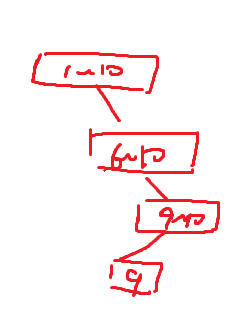
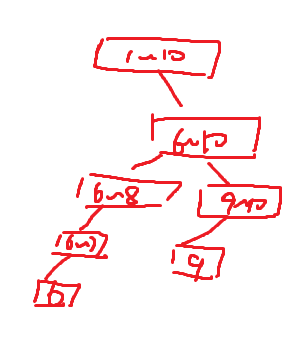
首先我们知道要开一个普通的线段树至少需要元素个数的$4$倍，对于这道题，如果对每一个宗教都开一个线段树显然不行，我们要对线段树进行改变，只保留树上有用的节点，单独用两个数组存左右儿子，查询时，遇到空区就直接返回，下面是两个图，可以帮助大家理解($Drawn$ $by$ $zyb$)

修改9

再修改6

但这种线段树的空间再不超出限制的情况下尽量开最大，否则会$\mathrm{RE}$或$\mathrm{WA}$

修改函数两个，一个是把原来的去掉，另一个是加上新的内容，请读者根据$code$自行理解。。。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define gc getchar()
#define pc(x) putchar(x)
#define re register
const int Maxn = 1e5 + 10;
inline int sc() {
    int xx = 0, ff = 1; char cch = gc;
    while(!isdigit(cch)) {
        if(cch == '-') ff = -1; cch = gc;
    }
    while(isdigit(cch)) {
        xx = (xx << 1) + (xx << 3) + (cch ^ '0'); cch = gc;
    }
    return xx * ff;
}
inline void out(int x) {
    if(x < 0) pc('-'), x = -x;
    if(x >= 10)
        out(x / 10);
    pc(x % 10 + '0');
}
struct node {
	int next, to;
}t[Maxn << 1];
struct LST {
	int sum, maxx, l, r;
}lst[Maxn * 40];
int n, m, cnt, len;
int w[Maxn], c[Maxn], head[Maxn], root[Maxn];
int siz[Maxn], top[Maxn], fa[Maxn], dep[Maxn], son[Maxn], id[Maxn];
inline void ADD(int from, int to) {
	t[++cnt].next = head[from];
	t[cnt].to = to;
	head[from] = cnt;
}
inline void dfs1(int now, int Fa, int Dep) {
	fa[now] = Fa;
	dep[now] = Dep;
	siz[now] = 1;
	for(re int i = head[now]; i; i = t[i].next) {
		int to = t[i].to;
		if(to == Fa) continue;
		dfs1(to, now, Dep + 1);
		siz[now] += siz[to];
		if(siz[son[now]] < siz[to])
			son[now] = to;
	}
}
inline void dfs2(int now, int topf) {
	id[now] = ++cnt;
//	rid[cnt] = now;
	top[now] = topf;
	if(!son[now]) return;
	dfs2(son[now], topf);
	for(re int i = head[now]; i; i = t[i].next) {
		int to = t[i].to;
		if(to == son[now] || to == fa[now]) continue;
		dfs2(to, to);
	}
}
inline void modify(int &k, int l, int r, int x, int z) {
	if(!k) k = ++len;
	lst[k].maxx = std :: max(lst[k].maxx, z), lst[k].sum += z;
	if(l == r) return;
	int mid = l + r >> 1;
	if(x <= mid) modify(lst[k].l, l, mid, x, z);
	else modify(lst[k].r, mid + 1, r, x, z);
}
inline void push(int &k, int l, int r, int x) {
	if(l == r) {
		lst[k].maxx = lst[k].sum = 0;
		return;
	}
	int mid = l + r >> 1;
	if(x <= mid) push(lst[k].l, l, mid, x);
	else push(lst[k].r, mid + 1, r, x);
	lst[k].maxx = std :: max(lst[lst[k].l].maxx, lst[lst[k].r].maxx);
	lst[k].sum = lst[lst[k].l].sum + lst[lst[k].r].sum;
}
inline int querymax(int k, int l, int r, int x, int y) {
	if(x > r || l > y) return 0;
	if(x <= l && r <= y) {
		return lst[k].maxx;
	}
	int mid = l + r >> 1;
	return std :: max(querymax(lst[k].l, l, mid, x, y), querymax(lst[k].r, mid + 1, r, x, y));
}
inline int querysum(int k, int l, int r, int x, int y) {
	if(x > r || l > y) return 0;  //y < l || x > r
	if(x <= l && r <= y) { //y >= r && x <= l  xlry
		return lst[k].sum;
	}
	int mid = l + r >> 1;
	return querysum(lst[k].l, l, mid, x, y) + querysum(lst[k].r, mid + 1, r, x, y);
}
inline int qymax(int x, int y, int cc) {
	int ans = 0;
	while(top[x] != top[y]) {
		if(dep[top[x]] < dep[top[y]]) std :: swap(x, y);
		ans = std :: max(ans, querymax(root[cc], 1, n, id[top[x]], id[x]));
		x = fa[top[x]];
	}
	if(dep[x] > dep[y]) std :: swap(x, y);
	ans = std :: max(ans, querymax(root[cc], 1, n, id[x], id[y]));
	return ans;
}
inline int qysum(int x, int y, int cc) {
	int ans = 0;
	while(top[x] != top[y]) {
		if(dep[top[x]] < dep[top[y]]) std :: swap(x, y);
		ans += querysum(root[cc], 1, n, id[top[x]], id[x]);
		x = fa[top[x]];
	}
	if(dep[x] > dep[y]) std :: swap(x, y);
	ans += querysum(root[cc], 1, n, id[x], id[y]);
	return ans;
}
int main() {
	n = sc(), m = sc();
	for(re int i = 1; i <= n; ++i)
		w[i] = sc(), c[i] = sc();
	for(re int i = 1; i < n; ++i) {
		int x = sc(), y = sc();
		ADD(x, y), ADD(y, x);
	}
	cnt = 0;
	dfs1(1, 0, 1), dfs2(1, 1);
	for(re int i = 1; i <= n; ++i)
		modify(root[c[i]], 1, n, id[i], w[i]);
	while(m--) {
		char ccc[5];
		std :: cin >> ccc;
		int x = sc(), y = sc();
		if(ccc[0] == 'C') {
			if(ccc[1] == 'C') {
//				std :: cerr << root[c[x]] << std :: endl;
				push(root[c[x]], 1, n, id[x]);
				modify(root[y], 1, n, id[x], w[x]);
				c[x] = y;
			}
			else {
//				std :: cerr << root[c[x]] << std :: endl;
				push(root[c[x]], 1, n, id[x]);
				modify(root[c[x]], 1, n, id[x], y);
				w[x] = y;
			}
		}
		else {
			if(ccc[1] == 'S') {
				out(qysum(x, y, c[x])), pc('\n');
			}
			else {
				out(qymax(x, y, c[x])), pc('\n');
			}
		}
	}
    return 0;
}
// Coded by dy.

rp++