浅谈Treap

发表于 分类于

Problem’s Website

普通平衡树

Solution

首先这道题可以用多种方法来解决，本篇题解用的是最low的$Treap$，以后可能会另外说明其他几种解法。

$BST$

在讲$Treap$之前，我们先来说一下二叉搜索树。

二叉搜索树($Binary$ $Search$ $Tree$，简称$BST$)，是一种具有特殊性质的二叉树。

性质：

1.树中的每个节点都有一个权值（先假设权值互不相同）

2.若左子树不为空，则左子树上所有节点的权值都小于它根节点的值。

3.若右子树不为空，则右子树上所有节点的权值都大于它根节点的值。

4.左右子树都为二叉搜索树。

类似于下图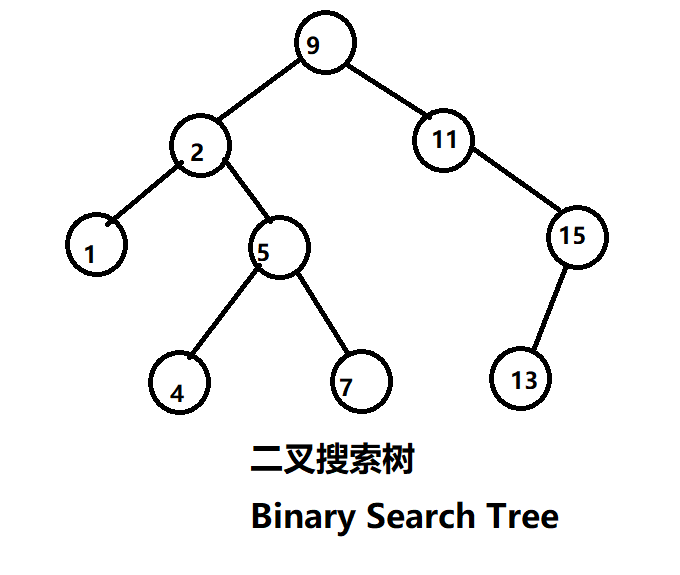

这种树可以支持多种动态集合操作，条件是所维护的集合存在大小关系。

$Treap$

现在我们步入正题，来说明$Treap$。

首先顾名思义，$Treap$ $=$ $Tree$ $+$ $Heap$，也就是树 + 堆，它既满足$BST$，又满足堆的性质。

我们思考一下，为什么要满足的堆的性质呢？

  • $Answer$: 现在如果有毒瘤出题人将集合中的元素都相等，那么$BST$是不是就退化成了一条链。那这样是不是很费时间？

那我们怎样使其满足堆的性质呢？

  • $Answer$：我们可以在每个节点上在rand一个数，确定节点的优先级。

接下来，为了使$Treap$满足要求，我们在必要时需要调整树的结构，那就是旋转。

分为两种，左旋和右旋。

  • 左旋($Zig$)：
    左旋一棵子树，我们假设这棵树的根节点为$x$，则旋转后$x$成为这棵子树的新根的左子节点，$x$的右子节点会成为子树新的根。

  • 右旋($Zag$):
    右旋一棵子树，我们假设这棵树的根节点为$x$，则旋转后$x$成为这棵子树的新根的右子节点，$x$的左子节点会成为子树新的根。

画个图感性理解一下：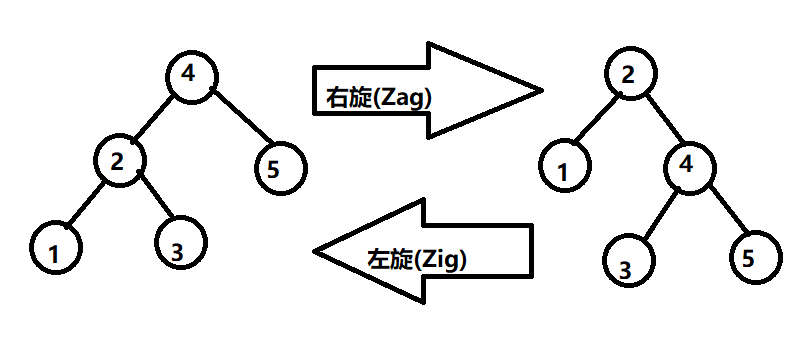

显然，旋转后的$Treap$仍然满足$BST$和堆的性质。

我们现在看一下code

1
2
3
4
5
6
7
8
inline void rotate(int &id, int dir) { //id为旋转节点编号，即上文x dir为旋转方向，0为Zig，1为Zag。
	int temp = treap[id][dir ^ 1]; //treap[id][0]为根编号为id的左子树，treap[id][1]为右子树。
	treap[id][dir ^ 1] = treap[temp][dir];
	treap[temp][dir] = id;
	id = temp;
	pushup(treap[id][dir]); //pushup为维护一些树的信息，下文会有解释。
	pushup(id);
}

现在我们来根据题目讲一下$Treap$的一些基本操作。

  • $Treap$插入元素

1.如果当前节点没有元素，就新建一个。

2.如果有重复的元素，计数器要$+1$。

3.否则，如果左子节点的优先级小于当前节点的优先级，就$Zag$，反之，就$Zig$。

下面是code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
inline void insert(int &id, int v) {
	if(!id) {
		id = cre(v); //cre函数为新建节点，下文会有解释。
		return;
	}
	if(v == val[id]) //val为当前节点的权值。
		++cnt[id]; //cnt为计数器，计算重复节点的出现次数。
	else {
		int dir = v < val[id] ? 0 : 1;
		insert(treap[id][dir], v);
		if(dat[id] < dat[treap[id][dir]]) //dat为rand的值
			rotate(id, dir ^ 1);
	}
	pushup(id);
}

给个图感性理解下吧~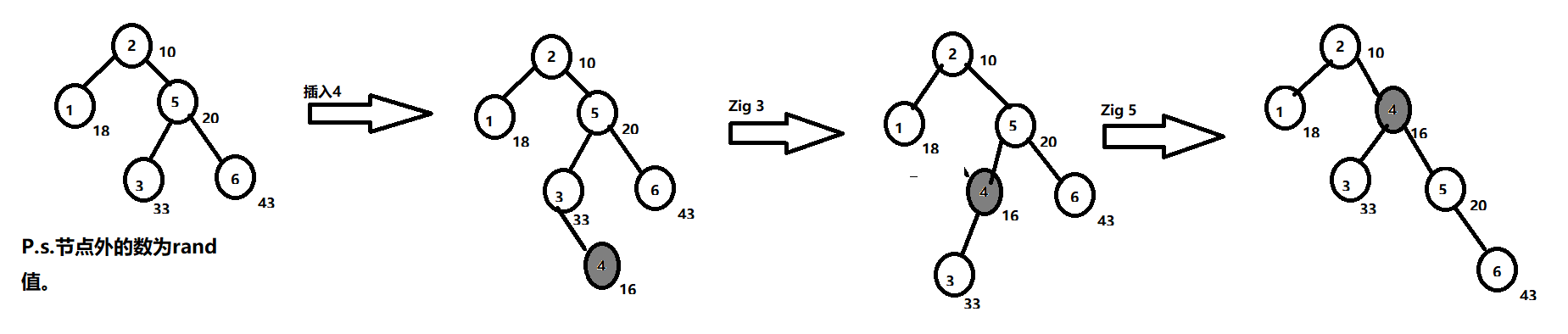

  • $Treap$删除元素

$Situation$ $1$: 没有该节点，直接返回。

$Situation$ $2$: 该节点的值有重复，计数器$-1$。

$Situation$ $3$: 该节点有且只有一颗子树

如果只有左子树或左子树优先级大于右子树，就$Zag$（因为只能$Zag$），然后遍历右子树。

否则，就$Zig$，然后遍历左子树。

$Situation$ $4$: 该节点有两颗子树，直接删除。

别忘了根据$BST$的性质进行遍历。

下面是code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
inline void Delete(int &id, int v) {
	if(!id)
		return;
	if(v == val[id]) {
		if(cnt[id] > 1) {
			--cnt[id];
			pushup(id);
			return;
		}
		if(treap[id][0] || treap[id][1]) {
			if(!treap[id][1] || dat[treap[id][0]] > dat[treap[id][1]]) {
				rotate(id, 1);
				Delete(treap[id][1], v);
			}
			else {
				rotate(id, 0);
				Delete(treap[id][0], v);
			}
			pushup(id);
		}
		else
			id = 0;
		return;
	}
	if(v < val[id])
		Delete(treap[id][0], v);
	else
		Delete(treap[id][1], v);
	pushup(id);
}

感觉删除操作还是比较好理解的，就不给图了。。。

  • $Treap$建树

其实这个步骤可以省略，但在本篇题解中，建树会影响下面的操作，所以有必要说明一下。

就是在树上建一个最大值和一个最小值。

直接上code

1
2
3
4
inline void build() {
	rt = cre(-INF), treap[rt][1] = cre(INF);
	pushup(rt);
}

顺便说一下cre函数和pushup函数吧，感觉不需要解释。。。

code如下

1
2
3
4
inline int cre(int v) {
	val[++tot] = v, dat[tot] = rand(), siz[tot] = cnt[tot] = 1; //siz为子树大小
	return tot;
}

1
2
3
inline void pushup(int id) {
	siz[id] = siz[treap[id][0]] + siz[treap[id][1]] + cnt[id];
}
  • $Treap$得到排名

$Situation$ $1$: 如果没有该节点，返回0。

$Situation$ $2$: 如果找到该节点，返回该节点左子树的大小$+1$。

$Situation$ $3$: 如果当前值小于左节点，则遍历左子树。

$Situation$ $4$: 否则，在遍历右子树的同时要加上左子树大小和重复的个数。(因为左子树都比该数小)

code

1
2
3
4
5
6
7
8
9
10
inline int get_rank(int id, int v) {
	if(!id)
		return 0;
	if(v == val[id])
		return siz[treap[id][0]] + 1;
	else if(v < val[id])
		return get_rank(treap[id][0], v);
	else
		return siz[treap[id][0]] + cnt[id] + get_rank(treap[id][1], v);
}

  • $Treap$得到排名第几的元素

$Situation$ $1$: 如果没有该节点，返回0。

$Situation$ $2$: 如果排名$\le$左子树的大小，就遍历左子树。

$Situation$ $3$: 如果排名$\le$左子树大小$+$重复的元素，就返回该节点。(说明答案就在中区间中)

$Situation$ $4$: 否则，遍历右子树，但排名要减去左子树大小$+$重复元素个数。

code

1
2
3
4
5
6
7
8
9
10
inline int get_val(int id, int rank) {
	if(!id)
		return 0;
	if(rank <= siz[treap[id][0]])
		return get_val(treap[id][0], rank);
	else if(rank <= siz[treap[id][0]] + cnt[id])
		return val[id];
	else
		return get_val(treap[id][1], rank - siz[treap[id][0]] - cnt[id]);
}

  • $Treap$得到前驱或后驱

思路其实是一样的，只是操作有些小区别，所以只说明求前驱，后驱请读者根据code自行理解。

循环求解，一直查到该节点不存在为止

循环过程中，如果当前节点比目标小，那就往右子树走。

否则，就往左子树走。

注意，做好记录。

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
inline int get_pre(int v) { //求前驱
	int id = rt, pre;
	while(id) {
		if(val[id] < v)
			pre = val[id], id = treap[id][1];
		else
			id = treap[id][0];
	}
	return pre;
}
inline int get_next(int v) { //求后驱
	int id = rt, nxt;
	while(id) {
		if(val[id] > v)
			nxt = val[id], id = treap[id][0];
		else
			id = treap[id][1];
	}
	return nxt;
}

OK，$Treap$的基本操作就讲完了。

最后是整个题目的具体代码。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define gc getchar()
#define pc(x) putchar(x)
#define re register
const int Maxn = 100000 + 10;
const int INF = 1e9;
inline int sc() {
    int xx = 0, ff = 1; char cch = gc;
    while(!isdigit(cch)) {
        if(cch == '-') ff = -1; cch = gc;
    }
    while(isdigit(cch)) {
        xx = (xx << 1) + (xx << 3) + (cch ^ '0'); cch = gc;
    }
    return xx * ff;
}
inline void out(int x) {
    if(x < 0) pc('-'), x = -x;
    if(x >= 10)
        out(x / 10);
    pc(x % 10 + '0');
}
int n;
int rt, tot;
int treap[Maxn][2], val[Maxn], dat[Maxn], siz[Maxn], cnt[Maxn];
inline int cre(int v) {
	val[++tot] = v, dat[tot] = rand(), siz[tot] = cnt[tot] = 1;
	return tot;
}
inline void pushup(int id) {
	siz[id] = siz[treap[id][0]] + siz[treap[id][1]] + cnt[id];
}
inline void build() {
	rt = cre(-INF), treap[rt][1] = cre(INF);
	pushup(rt);
}
inline void rotate(int &id, int dir) {
	int temp = treap[id][dir ^ 1];
	treap[id][dir ^ 1] = treap[temp][dir];
	treap[temp][dir] = id;
	id = temp;
	pushup(treap[id][dir]);
	pushup(id);
}
inline void insert(int &id, int v) {
	if(!id) {
		id = cre(v);
		return;
	}
	if(v == val[id])
		++cnt[id];
	else {
		int dir = v < val[id] ? 0 : 1;
		insert(treap[id][dir], v);
		if(dat[id] < dat[treap[id][dir]])
			rotate(id, dir ^ 1);
	}
	pushup(id);
}
inline void Delete(int &id, int v) {
	if(!id)
		return;
	if(v == val[id]) {
		if(cnt[id] > 1) {
			--cnt[id];
			pushup(id);
			return;
		}
		if(treap[id][0] || treap[id][1]) {
			if(!treap[id][1] || dat[treap[id][0]] > dat[treap[id][1]]) {
				rotate(id, 1);
				Delete(treap[id][1], v);
			}
			else {
				rotate(id, 0);
				Delete(treap[id][0], v);
			}
			pushup(id);
		}
		else
			id = 0;
		return;
	}
	if(v < val[id])
		Delete(treap[id][0], v);
	else
		Delete(treap[id][1], v);
	pushup(id);
}
inline int get_rank(int id, int v) {
	if(!id)
		return 0;
	if(v == val[id])
		return siz[treap[id][0]] + 1;
	else if(v < val[id])
		return get_rank(treap[id][0], v);
	else
		return siz[treap[id][0]] + cnt[id] + get_rank(treap[id][1], v);
}
inline int get_val(int id, int rank) {
	if(!id)
		return 0;
	if(rank <= siz[treap[id][0]])
		return get_val(treap[id][0], rank);
	else if(rank <= siz[treap[id][0]] + cnt[id])
		return val[id];
	else
		return get_val(treap[id][1], rank - siz[treap[id][0]] - cnt[id]);
}
inline int get_pre(int v) {
	int id = rt, pre;
	while(id) {
		if(val[id] < v)
			pre = val[id], id = treap[id][1];
		else
			id = treap[id][0];
	}
	return pre;
}
inline int get_next(int v) {
	int id = rt, nxt;
	while(id) {
		if(val[id] > v)
			nxt = val[id], id = treap[id][0];
		else
			id = treap[id][1];
	}
	return nxt;
}
int main() {
	build();
	n = sc();
	while(n--) {
		int opt = sc(), x = sc();
		if(opt == 1)
			insert(rt, x);
		else if(opt == 2)
			Delete(rt, x);
		else if(opt == 3)
			out(get_rank(rt, x) - 1), pc('\n'); //注意，因为我们之前建树时已经插入了一个最大值和一个最小值，所以求排名和第几大是要稍加修改。
		else if(opt == 4)
			out(get_val(rt, x + 1)), pc('\n'); //即求排名是得到的答案要-1，求第几大时要+1。
		else if(opt == 5)
			out(get_pre(x)), pc('\n');
		else
			out(get_next(x)), pc('\n');
	}
    return 0;
}
// Coded by dy.

rp++