Processing math: 100%

浅谈fhq-Treap

发表于 分类于

Problem’s Website

普通平衡树（洛谷）

普通平衡树（LOJ）

Solution

没错，又是这道题。

再上一篇题解中，我们介绍了使用Treap的做法，那么本篇题解讲解一下fhq−Treap的做法。

先来普及一下，fhq−Treap由OI界的著名DALAO范浩强发明，至于他有多巨，看图吧。

他不仅OI强，人其实也挺 handsome 的。

P.s.该图片来源毕业季 | 范浩强：游走在学业和科研间的清华创客

好了，我们步入正题。

fhq−Treap又叫无旋Treap，顾名思义，就是没有旋转的Treap，取而代之的是分裂和合并，正因如此，fhq−Treap可以解决Treap解决不了的区间问题，而且还可以持久化，这些内容以后我会另外介绍。

首先，我们先明确下文中代码变量的意思。

1
2
3
4
int siz[Maxn], val[Maxn], dat[Maxn], ch[Maxn][2];
int x, y, z, tot, rt;
//siz为子树大小，val为节点权值，dat为rand值，ch记录左右儿子（0为左儿子，1为右儿子）。
// x,y,z为暂定的左右儿子编号，tot为总共的节点数，rt为当前树的根节点编号。

在说明基本操作前，我们先来说一下fhq−Treap的一些核心思想及操作

  • 分裂

分裂分为两种，一种为权值分裂，另一种为排名分裂。

权值分裂

我们现在遍历到一个点，如果它的权值小于v，那么它的左子树会被分到左边的树里，然后我们遍历它的右儿子，如果大于v，则把它的右子树分到右边的树里。

那出现了一个小问题：如果到达递归边界id==0怎么办呢？

那我们就初始化一下，令x=y=0

如果遍历到了叶子节点，我们就返回。

注意，对于形参中的x,y要取地址，这样就可以直接更新全局变量x,y。

看下代码吧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
inline void split(int id, int v, int &x, int &y) {
	if(!id)
		x = y = 0;
	else {
		if(val[id] <= v) {
			x = id;
			split(ch[id][1], v, ch[id][1], y);
		}
		else {
			y = id;
			split(ch[id][0], v, x, ch[id][0]);
		}
		pushup(id);
	}
}

排名分裂

与权值分裂类似，把权值当成排名(siz)即可。

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
inline void split(int id, int r, int &x, int &y) {
    if(!id)
        x=y=0;
    else {
        if(r <= siz[ch[id][0]]) {
            y = id;
            split(ch[id][0], r, x, ch[id][0]);
        }
        else {
            x = id;
            split(ch[id][1], r - siz[ch[id][0]] - 1, ch[id][1], y);
        }
        pushup(id);
    }
}

给个图感性理解一下：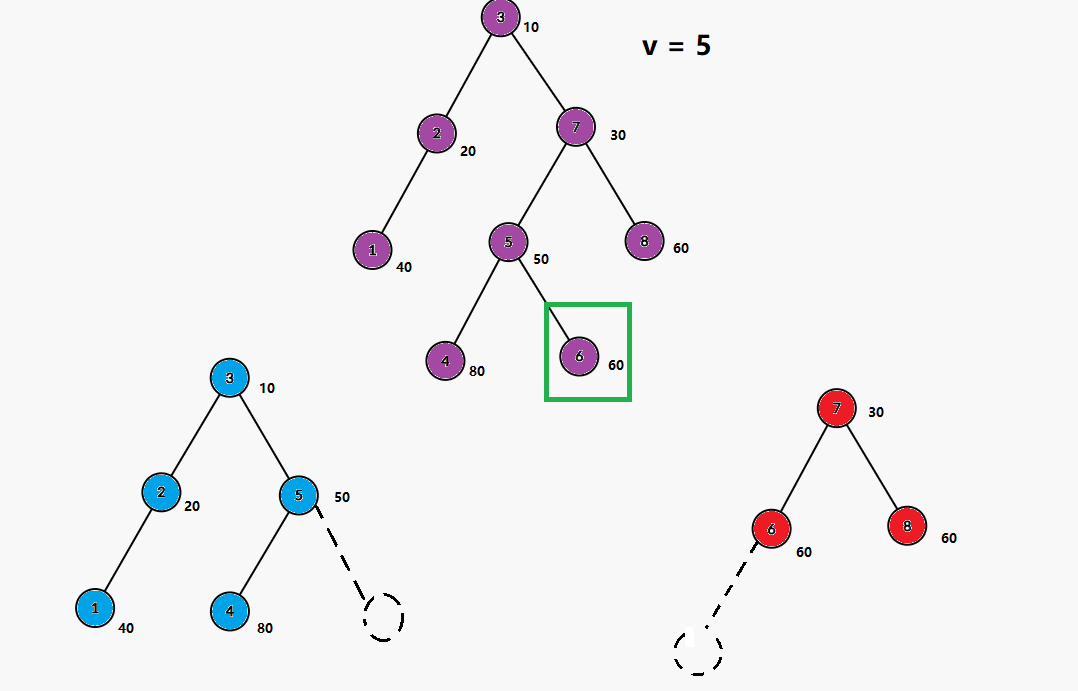

  • 合并

我们假设第一棵树的权值小于第二棵树的权值，那么我们就比较它们的随机权值。如果dat[l]<dat[r]，我们就保留它的左子树，另一棵树作为它的右子树；如果dat[l]≥dat[r]，那我们可以保留第二棵树的右子树，另一颗树作为它的左子树。

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
inline int merge(int A, int B) {
	if(!A || !B)
		return A + B;
	if(dat[A] < dat[B]) {
		ch[A][1] = merge(ch[A][1], B);
		pushup(A);
		return A;
	}
	else {
		ch[B][0] = merge(A, ch[B][0]);
		pushup(B);
		return B;
	}
}

图示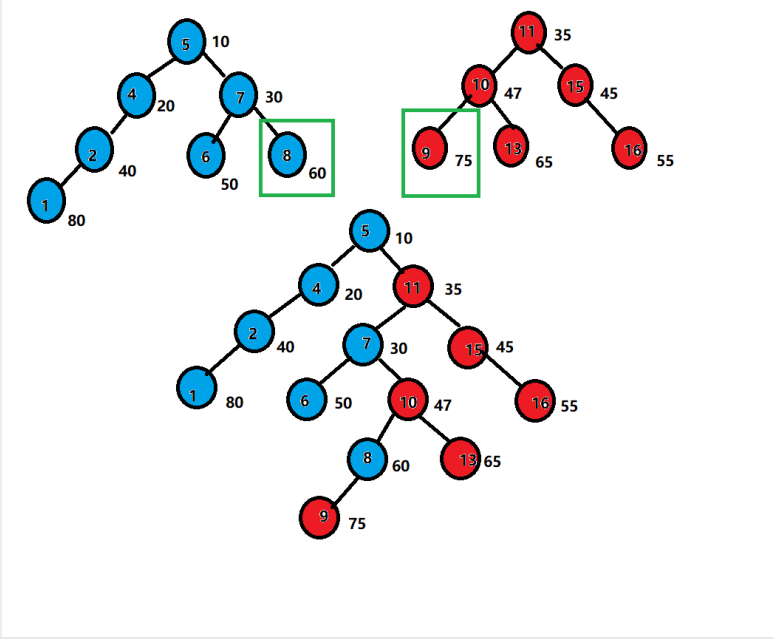

现在我们开始介绍fhq−Treap的一些基本操作。

  • pushup

合并子树大小。

code

1
2
3
inline void pushup(int id) {
	siz[id] = siz[ch[id][0]] + siz[ch[id][1]] + 1;
}
  • 插入

直接merge即可

code

1
2
3
4
5
6
7
8
inline int cre(int v) {
	siz[++tot] = 1, val[tot] = v, dat[tot] = rand();
	return tot;
}
inline void insert(int v) {
	split(rt, v, x, y);
	rt = merge(merge(x, cre(v)), y);
}
  • 删除

删除权值为v的点，先把整颗树以v为权值分裂成两棵树a,b,再把a树按照v−1分成c,d。这时候值为v的点一定为d的根，那么我们把d的两个子儿子merge起来（划重点：这一步就是去除掉v的影响），再把他们重新merge起来得到一个新的树，这颗树就去除掉了v的影响。

code

1
2
3
4
5
6
inline void Delete(int v) {
	split(rt, v, x, z);
	split(x, v - 1, x, y);
	y = merge(ch[y][0], ch[y][1]);
	rt = merge(merge(x, y), z);
}

  • 得到排名

直接按照v−1的权值把树分开，那么x树中最大的应该小于等于v−1，那么v的排名就是siz[x]+1。

code

1
2
3
4
5
6
inline int get_rank(int v) {
	split(rt, v - 1, x, y);
	int res = siz[x] + 1;
	rt = merge(x, y);
	return res;
}

  • 得到排名为几的数据

循环求解。

如果当前r≤左子树的大小，那么就往左子树找；如果r恰好等于左子树大小+ 1，说明就是当前节点；否则r减去(左子树大小 + 1)，然后去找右子树。

code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
inline int rank(int id, int r) {
	while(1) {
		if(r <= siz[ch[id][0]])
			id = ch[id][0];
		else if(r == siz[ch[id][0]] + 1)
			return id;
		else {
			r -= (siz[ch[id][0]] + 1);
			id = ch[id][1];
		}
	}
}

out(val[rank(rt, x)]), pc('\n'); //out为快输，pc为putchar。

  • 前驱后驱

因为两者具有很大的相似性，所以我们只讲找前驱，后驱请读者根据代码自行理解。

因为要小于v，所以我们还是按照v−1的权值划分x，现在x中最大的数一定小于等于v−1，所以我们直接输出x中最大的数就好。

code

1
2
3
4
5
6
7
8
9
10
11
12
inline int get_pre(int v) { //前驱
	split(rt, v - 1, x, y);
	int res = val[rank(x, siz[x])];
	rt = merge(x, y);
	return res;
}
inline int get_next(int v) { //后驱
	split(rt, v, x, y);
	int res = val[rank(y, 1)];
	rt = merge(x, y);
	return res;
}

本题的操作就讲完了，当然fhq−Treap不止这些东西，以后根据题目再说明吧。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define gc getchar()
#define pc(x) putchar(x)
#define re register
const int Maxn = 1e5 + 10;
inline int sc() {
    int xx = 0, ff = 1; char cch = gc;
    while(!isdigit(cch)) {
        if(cch == '-') ff = -1; cch = gc;
    }
    while(isdigit(cch)) {
        xx = (xx << 1) + (xx << 3) + (cch ^ '0'); cch = gc;
    }
    return xx * ff;
}
inline void out(int x) {
    if(x < 0) pc('-'), x = -x;
    if(x >= 10)
        out(x / 10);
    pc(x % 10 + '0');
}
int n;
int siz[Maxn], val[Maxn], dat[Maxn], ch[Maxn][2];
int x, y, z, tot, rt;
inline void pushup(int id) {
	siz[id] = siz[ch[id][0]] + siz[ch[id][1]] + 1;
}
inline int cre(int v) {
	siz[++tot] = 1, val[tot] = v, dat[tot] = rand();
	return tot;
}
inline void split(int id, int v, int &x, int &y) {
	if(!id)
		x = y = 0;
	else {
		if(val[id] <= v) {
			x = id;
			split(ch[id][1], v, ch[id][1], y);
		}
		else {
			y = id;
			split(ch[id][0], v, x, ch[id][0]);
		}
		pushup(id);
	}
}
inline int merge(int A, int B) {
	if(!A || !B)
		return A + B;
	if(dat[A] < dat[B]) {
		ch[A][1] = merge(ch[A][1], B);
		pushup(A);
		return A;
	}
	else {
		ch[B][0] = merge(A, ch[B][0]);
		pushup(B);
		return B;
	}
}
inline void insert(int v) {
	split(rt, v, x, y);
	rt = merge(merge(x, cre(v)), y);
}
inline void Delete(int v) {
	split(rt, v, x, z);
	split(x, v - 1, x, y);
	y = merge(ch[y][0], ch[y][1]);
	rt = merge(merge(x, y), z);
}
inline int get_rank(int v) {
	split(rt, v - 1, x, y);
	int res = siz[x] + 1;
	rt = merge(x, y);
	return res;
}
inline int rank(int id, int r) {
	while(1) {
		if(r <= siz[ch[id][0]])
			id = ch[id][0];
		else if(r == siz[ch[id][0]] + 1)
			return id;
		else {
			r -= (siz[ch[id][0]] + 1);
			id = ch[id][1];
		}
	}
}
inline int get_pre(int v) {
	split(rt, v - 1, x, y);
	int res = val[rank(x, siz[x])];
	rt = merge(x, y);
	return res;
}
inline int get_next(int v) {
	split(rt, v, x, y);
	int res = val[rank(y, 1)];
	rt = merge(x, y);
	return res;
}
int main() {
	n = sc();
	while(n--) {
		int opt = sc(), x = sc();
		if(opt == 1)
			insert(x);
		else if(opt == 2)
			Delete(x);
		else if(opt == 3)
			out(get_rank(x)), pc('\n');
		else if(opt == 4)
			out(val[rank(rt, x)]), pc('\n');
		else if(opt == 5)
			out(get_pre(x)), pc('\n');
		else
			out(get_next(x)), pc('\n');
	}
    return 0;
}
// Coded by dy.

rp++

Gitalking ...