$Problem’s$ $Website$
$Solution$
这是一道平衡树的好题,因为我暂时不会$Splay$,所以我就用$fhq-Treap$来写。
首先关于$fhq-Treap$的一些解释在我的另外一篇blog中已经详细说明了,不懂的童鞋可以先去学习一下。
这道题要用到排名分裂,同样用到这种方法的还有另外一道同名题。
上面好像都是废话,下面是干货。
下面详细地说一下操作。
1.处理书的名称:
因为是字符串,所以我们用一个$string$类型的数组记录,用一个变量当做编号映射到每本书的名称。
温馨提示:注意数据范围,否则将惨遭$RE$。。。(好像就我这个菜鸡$RE$了)
2.处理一开始就在书架上的书:
我们所说的“排名”即当前这本书的上面有几本书,所以对于最开始的书籍,我们只要$insert(i - 1, cnt);$即可(cnt即为映射的变量)
3.处理后来放入的书籍:
经过研究样例,我们发现:插入一个位置为$x$的书,原本的第$x$本到最后一本的位置都会$+1$,也就是
,那么也就是说,插入后这本书的排名就为$x$,所以就$insert(x, cnt);$
4.处理询问
要输出第$x$个位置书的名称,我们就相当于找到第$x$个位置书映射的编号。
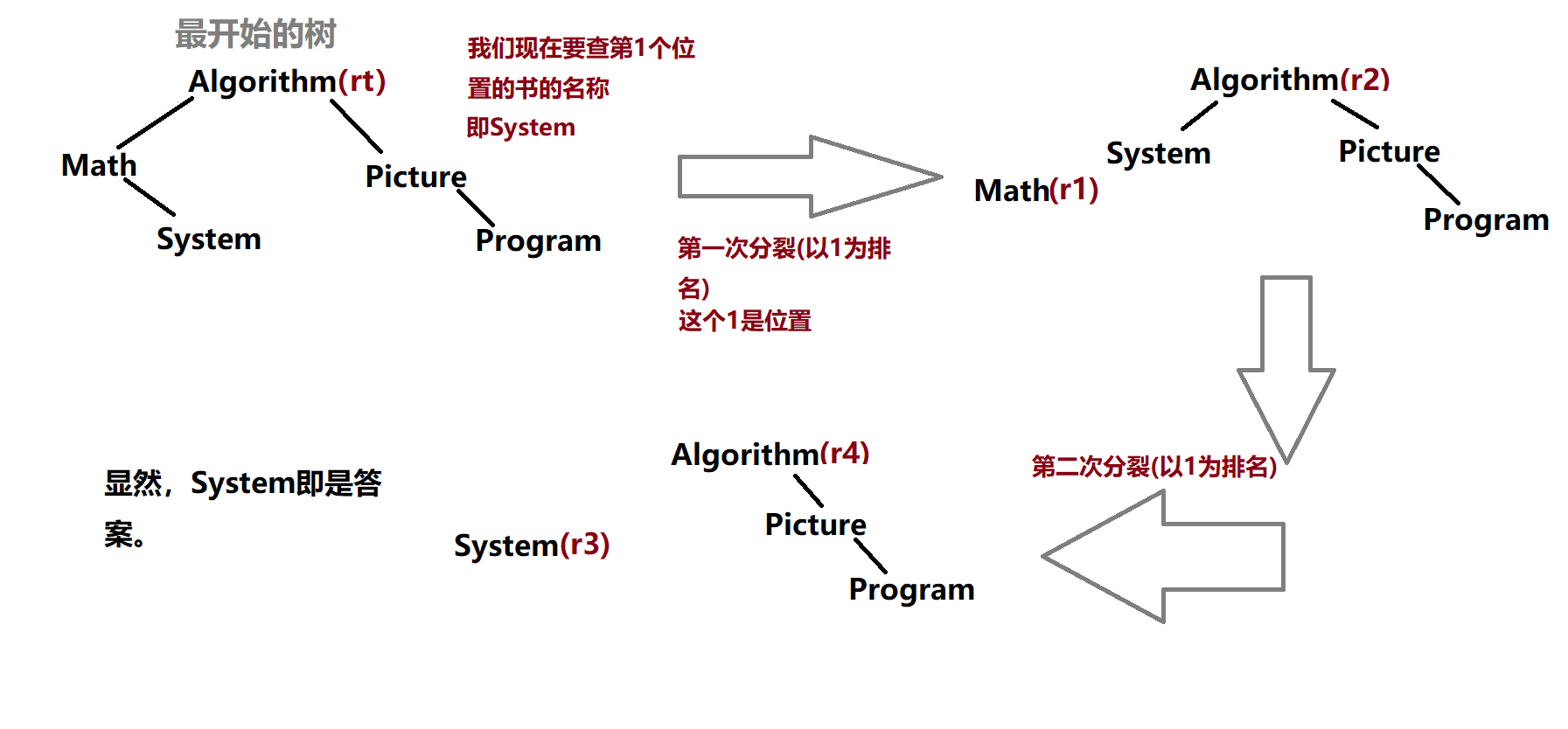
方法也很简单,我们首先以$x$为排名将树分裂成以$r1, r2$为根的两棵树,再对$r2$以$1$为排名分裂成以$r3, r4$为根的两棵树,这样$r3$就成了一个节点,也就是要求的答案。
给个图让大家理解一下(对于$fhq-Treap$,不理解的时候画个图有事半功倍的效果):
别忘了最后合并回去。
相信大家对$fhq-Treap$又加深了理解。
所以下面代码就不解释了 (逃
$Code$
1 | //Coded by dy. |
$rp++$