TJOI2013 最长上升子序列

发表于 分类于

$Problem’s$ $Website$

TJOI2013 最长上升子序列

$Solution$

这道题是一道既考思想有考代码能力的好题，能学到不少东西。

这道题我是用$fhq-Treap$ $+$ 线段树 做的，思想类似于模板 最长公共子序列，这道题我写了一篇题解，大家可以先去查看一下，当然也可以不看。。。

大体说一下做法

1.关于维护序列

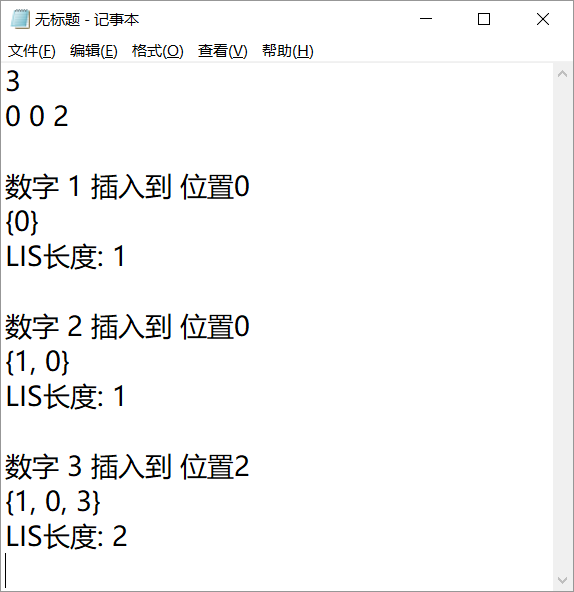
首先要把样例搞懂，所以我先把样例解释一下，见下图：

我们发现，将一个数组$x$插入到位置$i$，如果位置$i$已经有数字了，那么要进行右移，那么平衡树自然是维护序列的不二选择了，因为我暂时不会$Splay$，所以我用的是$fhq-Treap$。

对于$fhq-Treap$来说，有一点要注意，就是分裂的对象，这道题我们要以子树的大小为对象进行分裂。

2.求$LIS$

因为数据肯定不重复，所以我们可以用类似于离散化的方式来求$LIS$。

也就是用一个数组$a[x]$来记录数字$x$出现的位置，我们从小到大枚举 （因为要求$LIS$），每次求出从$1$到当前数字位置的前一个的$LIS$长度，$+1$后更新答案 （因为当前数一定比前面的数大），最后把当前位置的$LIS$记录下来。

上面的操作就是单点修改和区间最值，那么，线段树搞定!

$Code$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
//Coded by dy.
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define gc getchar()
#define pc(x) putchar(x)
#define re register
using std :: max;
const int Maxn = 100000 + 10;
inline int sc() {
	int xx = 0, ff = 1; char cch = gc;
	while(!isdigit(cch)) {
		if(cch == '-') ff = -1; cch = gc;
	}
	while(isdigit(cch)) {
		xx = (xx << 1) + (xx << 3) + (cch ^ '0'); cch = gc;
	}
	return xx * ff;
}
inline void out(int x) {
	if(x < 0)
		pc('-'), x = -x;
	if(x >= 10)
		out(x / 10);
	pc(x % 10 + '0');
}
struct fhq_Treap {
	int siz, val, dat;
	int ch[2];
}t[Maxn];
int n, ans;
int a[Maxn];
int lst[Maxn << 2];
int rt, r1, r2, tot;
inline void pushup(int id) {
	t[id].siz = t[t[id].ch[0]].siz + t[t[id].ch[1]].siz + 1;
}
inline int cre(int v) {
	t[++tot].siz = 1, t[tot].val = v, t[tot].dat = rand();
	return tot;
}
inline void split(int id, int k, int &x, int &y) {
	if(!id)
		x = y = 0;
	else {
		if(k <= t[t[id].ch[0]].siz) {
			y = id;
			split(t[id].ch[0], k, x, t[id].ch[0]);
		}
		else {
			x = id;
			split(t[id].ch[1], k - t[t[id].ch[0]].siz - 1, t[id].ch[1], y);
		}
		pushup(id);
	}
}
inline int merge(int x, int y) {
	if(!x || !y)
		return x + y;
	if(t[x].dat < t[y].dat) {
		t[x].ch[1] = merge(t[x].ch[1], y);
		pushup(x);
		return x;
	}
	t[y].ch[0] = merge(x, t[y].ch[0]);
	pushup(y);
	return y;
}
inline void insert(int val, int id) {
	split(rt, val, r1, r2);
	rt = merge(r1, merge(cre(id), r2));
}
inline int rank(int id, int r) {
	while(1) {
		if(r <= t[t[id].ch[0]].siz)
			id = t[id].ch[0];
		else if(r == t[t[id].ch[0]].siz + 1)
			return id;
		else {
			r -= (t[t[id].ch[0]].siz + 1);
			id = t[id].ch[1];
		}
	}
}
inline void modify(int k, int l, int r, int x, int z) {
	if(l == r && l == x) {
		lst[k] = z;
		return;
	}
	int mid = l + r >> 1;
	if(x <= mid)
		modify(k << 1, l, mid, x, z);
	else
		modify(k << 1 | 1, mid + 1, r, x, z);
	lst[k] = max(lst[k << 1], lst[k << 1 | 1]);
}
inline int query(int k, int l, int r, int x, int y) {
	if(x <= l && r <= y)
		return lst[k];
	int mid = l + r >> 1, res = 0;
	if(x <= mid)
		res = max(res, query(k << 1, l, mid, x, y));
	if(y > mid)
		res = max(res, query(k << 1 | 1, mid + 1, r, x, y));
	return res;
}
int main() {
	srand(20041029);
	n = sc();
	for(re int i = 1; i <= n; ++i)
		insert(sc(), i);
	for(re int i = 1; i <= n; ++i)
		a[t[rank(rt, i)].val] = i;
	for(re int i = 1; i <= n; ++i) {
		if(a[i] == 1) {
			ans = max(ans, 1);
			modify(1, 1, n, a[i], 1);
		}
		else {
			int temp = query(1, 1, n, 1, a[i] - 1) + 1;
			ans = max(ans, temp);
			modify(1, 1, n, a[i], temp);
		}
		out(ans), pc('\n');
	}
	return 0;
}

$rp++$